Estimation of an elastic net model, including options for Lasso and ridge regression.
Syntax
enet(options) y x1 [x2 x3 ...] [@vw(...)]
List the dependent variable first, followed by a list of the independent variables. Use a “C” if you wish to include an unpenalized intercept term.
Note that PDL and ARMA terms are not permitted in elastic net specifications.
If you wish to specify regressors with an individual penalty weight
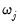
, or to place inequality restrictions on the coefficient values, you may do so using special expressions of the form:
@vw(series_name, weight_value)
or
@vw(series_name[, wgt=weight_value, cmin=coef_min, cmax=coef_max])
where weight_value is a non-negative value, coef_min is a non-positive minimum coefficient value, and coef_max is a non-negative maximum coefficient value.
There are two forms of the special expression.
In the abbreviated form, you specify the variable name followed by the penalty weight value.
In the more general form, you specify the variable name followed by one or more keyword expressions in arbitrary order, with the “wgt=” argument specifying the penalty weight, “cmin=” with a non-positive minimum coefficient value, and “cmax=” with a non-negative maximum coefficient value.
When specifying individual regressor behavior using @vw, keep in mind that:
• The special intercept variable “C” is always non-penalized and has an implicit weight
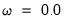
.
• Individual penalty weights may be also specified using a vector in the edit field on the dialog page (or using the command estimation option “lambdawgt=vector_name”). If the vector weights are specified and individual weights are specified using the @vw keyword, the vector weights will be applied first, followed by the individual variable weights.
• Individual coefficient limit values may also be specified using vectors in the and edit fields on the dialog page (or the command estimation options “coefmin=vector_name” and “coefmax=vector_name”). If vector coefficient limits are specified and individual regressor limits are specified using the @vw keyword, the vector limits will be applied first, followed by the individual limits weights.
EViews will normalize the individual penalty weights so that they sum to the number of coefficients.
Options
Specification Options
penalty=arg (default=“el”) | Type of threshold estimation: “enet” (elastic net), “ridge” (ridge), “lasso” (Lasso). |
alpha=arg (default=“.5”) | Value of the mixing parameter. Must be a value from zero to one. |
lambda=arg | Value(s) of the penalty parameter. Can be one or more numbers or vector objects.Values must be zero or greater. If left blank (default) EViews will generate a list. |
Penalty Options
ytrans=arg (default=“none”) | Scaling of the dependent variable: “none” (none), “L1” (L1), “L2” (L2), “stdsmpl” (sample standard deviation), “stdpop” (population standard deviation), “minmax” (min-max). |
xtrans=arg (default=“stdpop”) | Scaling of the regressor variables: “none” (none), “L1” (L1 norm), “L2” (L2 norm), “stdsmpl” (sample standard deviation), “stdpop” (population standard deviation), “minmax” (min-max). |
nlambdas=integer (default=100) | Number of penalty values for EViews-supplied list. |
lambdaratio=arg | Ratio of minimum to maximum lambda for EViews-supplied list. You may specify a value for the ratio parameter, or you may leave the edit field blank to let EViews specify a default value based on the number of observations 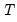 and the number of potential regressors 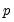 . By default, EViews will set the ratio to 0.001. |
lambdawgt= vector_name | Vector of individual penalty weights, containing non-negative values sized to and matching the order of the variables in the specification. If a vector is provided and individual weights are specified using one or more @vw regressors, the vector weights will be applied first, then overwritten by the individual variable weights. For comparability purposes, we normalize the final weights so that they sum to 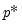 where 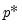 the number of non-zero 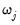 . |
nlambdamin=integer (default=5) | Minimum number of lambda values in the path before applying stopping rules. |
minddev=arg (default=1e-05) | Minimum change in deviance fraction to continue estimation. Truncate path estimation if relative change in deviance is smaller than this value. |
maxedev=arg (default=0.99) | Maximum of deviance explained fraction attained to terminate estimation. Truncate path estimation if fraction of null deviance explained is larger than this value. |
maxvars=arg | Maximum number of regressors in the model. Truncate path estimation if the number of coefficients (including those for non-penalized variables like the intercept) reaches this value. |
maxvarsratio=arg | Maximum number of regressors in the model as a fraction of the number of observations. Truncate path estimation if the number of coefficients (including those for non-penalized variables like the intercept) divided by the number of observations reaches this value. |
Cross Validation Options
cvmethod=arg (default=“kfold_cv”) | Cross-validation method: “kfold” (k-fold), “simple” (simple split), “mcarlo” (Monte Carlo), “leavepout” (leave-P-out), “leave1out” (leave-1-out), “rolling” (rolling window), “expanding” (expanding window). |
cvmeasure=arg (default=“mse”) | Cross-validation fit measure: “mse” (mean-squared error), “r2” (R‑squared), “mae” (mean absolute error), “mape” (mean absolute percentage error), “smape” (symmetric mean absolute percentage error). |
cvnfolds=arg (default=5) | Number of folds for K-fold cross-validation. For “cvmethod=kfold”. |
cvftrain=arg (default=0.8) | Proportion of data for split and Monte Carlo methods. For “cvmethod=simple” and “cvmethod=mcarlo”. |
cvnreps=arg (default=1) | Number of Monte Carlo method repetitions. For “cvmethod=mcarlo”. |
cvleaveout=arg (default=2) | Number of data points left out for leave-p-out method. For “cvmethod=leavepout”. |
cvnwindows=arg (default=4) | Number of windows for rolling window cross-validation method. For “cvmethod=rolling”. |
cvinitial=arg (default=12) | Number of initial data points in the training set for expanding cross-validation. For “cvmethod=expanding”. |
cvpregap=arg (default=0) | Number of observations between end of training set and beginning of test set. For “cvmethod=simple”, “cvmethod=rolling” and “cvmethod=expanding”. |
cvhorizon=arg (default=1) | Number of observation in the test set. For “cvmethod=rolling” and “cvmethod=expanding”. |
cvpostgap=arg (default=0) | Number of observations between end of test set and beginning of next training set for rolling window or between end of test set and end of next training set for expanding window. For “cvmethod=rolling” and “cvmethod=expanding” |
Random Number Options
seed=positive_integer from 0 to 2,147,483,647 | Seed the random number generator. If not specified, EViews will seed random number generator with a single integer draw from the default global random number generator. |
rnd= arg (default=“kn” or method previously set using
rndseed). | Type of random number generator: improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4”) L’Ecuyer’s (1999) combined multiple recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). |
Other Options
coefmin= vector_name, number | Vector of individual coefficient minimum values, containing negative or missing values sized to and matching the order of the variables in the specification, or a negative value for the minimum for all coefficients. Missing values in the vector should be used to indicate that the coefficient is unrestricted. If a vector of values is provided and individual minimums are specified using one or more @vw regressors, the vector values will be applied first, then overwritten by the individual values. |
coefmax= vector_name, number | Vector of individual coefficient maximum values, containing positive or missing values sized to and matching the order of the variables in the specification, or a positive value for the maximum for all coefficients. Missing values in the vector should be used to indicate that the coefficient is unrestricted. If a vector of values is provided and individual maximums are specified using one or more @vw regressors, the vector values will be applied first, then overwritten by the individual values. |
maxit=integer | Maximum number of iterations. |
conv=scalar | Set convergence criterion. The criterion is based upon the maximum of the percentage changes in the scaled estimates. The criterion will be set to the nearest value between 1e-24 and 0.2. |
w=arg | Weight series or expression. |
wtype=arg (default=“istdev”) | Weight specification type: inverse standard deviation (“istdev”), inverse variance (“ivar”), standard deviation (“stdev”), variance (“var”). |
wscale=arg | Weight scaling: EViews default (“eviews”), average (“avg”), none (“none”). The default setting depends upon the weight type: “eviews” if “wtype=istdev”, “avg” for all others. |
showopts / ‑showopts | [Do / do not] display estimation options in the output. |
prompt | Force the dialog to appear from within a program. |
p | Print basic results view after estimation. |
Examples
The command
enet(xtrans=none, lambdaratio=.0001, cvseed=513255899) lpsa c lcavol lweight age lbph svi lcp gleason pgg45
estimates an elastic net model with
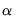
equal to the default of 0.9, no regressor or dependent variable scaling, automatically determined 100-element lambda path with minimum lambda of 0.0001 times the maximum value, using the default K-fold cross-validation with 5 folds with an MSE objective and a random generator seed of 513255899 to determine the optimal value.
Similarly,
enet(penalty=lasso, lambdaratio=.0001, cvseed=513255899) lpsa c lcavol lweight age lbph svi lcp gleason pgg45
estimates a Lasso model with regressor population standard deviation scaling, with the remaining settings as before, while
enet(penalty=ridge, lambdaratio=.0001, cvseed=513255899) lpsa c lcavol lweight age lbph svi lcp gleason pgg45
estimates the equivalent ridge regression specification.
The command
enet(alpha=0.75, lambdaratio=.0001, cvmethod=rolling, cvmeasure=smape) lpsa c lcavol lweight age_s lbph svi lcp gleason pgg45
estimates an elastic net model with

equal to the 0.75 using rolling window cross-validation and SMAPE cross-validation.
We may use the @vw specifications to assign individual penalties and coefficient restrictions
enet(alpha=0.75, lambdaratio=.0001, cvmethod=rolling, cvseed=513255899) lpsa c @vw(lcavol, cmax=.4) lweight age lbph svi lcp gleason @vw(pgg45, cmax=0.075, w=1.2)
estimates an elastic net model with the coefficient of LCAVOL restricted to be less than or equal to 0.4, and the coefficient of PGG45 having a relative penalty weight of 1.2, and a maximum value of 0.075.
Identical specifications may be estimated using vectors of penalty weights and coefficient restrictions,
vector(9) cmax = na
cmax(2) = 0.4
cmax(9) = 1.2
vector(9) lwgt = 1
lwgt(9) = 1.2
enet(alpha=0.75, coefmax=cmax, lambdawgt=lwgt, lambdaratio=.0001, cvmethod=rolling, cvseed=513255899) lpsa c lcavol lweight age lbph svi lcp gleason pgg45
and
vector(9) cmax = na
cmax(2) = 0.4
vector(9) lwgt = 1
lwgt(9) = 50
enet(alpha=0.75, coefmax=cmax, lambdawgt=lwgt, lambdaratio=.0001, cvmethod=rolling, cvseed=513255899) lpsa c lcavol lweight age lbph svi lcp gleason @vw(pgg45, cmax=0.075, w=1.2)
since the penalty weight for PGG45 in the vector is overwritten by the individual weight specified using the @vw.
Note that in neither case is the intercept penalized, even though the corresponding element of LWGT is equal to 1 since the specification of “C” is always implicitly treated as “@VW(C, 0)”.
Cross-references
See
“Elastic Net and Lasso” for a discussion of elastic net, ridge regression, and Lasso models.
See
Equation::enet for the object version of this command.
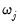 , or to place inequality restrictions on the coefficient values, you may do so using special expressions of the form:
, or to place inequality restrictions on the coefficient values, you may do so using special expressions of the form: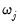 , or to place inequality restrictions on the coefficient values, you may do so using special expressions of the form:
, or to place inequality restrictions on the coefficient values, you may do so using special expressions of the form: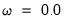 .
.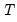 and the number of potential regressors
and the number of potential regressors 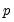 .
.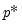 where
where 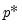 the number of non-zero
the number of non-zero 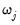 .
. 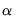 equal to the default of 0.9, no regressor or dependent variable scaling, automatically determined 100-element lambda path with minimum lambda of 0.0001 times the maximum value, using the default K-fold cross-validation with 5 folds with an MSE objective and a random generator seed of 513255899 to determine the optimal value.
equal to the default of 0.9, no regressor or dependent variable scaling, automatically determined 100-element lambda path with minimum lambda of 0.0001 times the maximum value, using the default K-fold cross-validation with 5 folds with an MSE objective and a random generator seed of 513255899 to determine the optimal value. equal to the 0.75 using rolling window cross-validation and SMAPE cross-validation.
equal to the 0.75 using rolling window cross-validation and SMAPE cross-validation.