Additional Testing
Note that the above specification has been selected for illustration purposes only. Indeed, performing various specification tests on EQLAGS suggests that there may be a number of problems with the existing specification.
For one, there is quite a bit of serial correlation remaining even after estimating the lag specification. A test of serial correlation in the EQLAGS equation (by selecting , and entering “1” for the number of lags) rejects the null hypothesis of no serial correlation in the reformulated equation. The top portion of the output is:
Moreover, there is strong evidence of autoregressive conditional heteroskedasticity (ARCH) in the residuals. Select to bring up the dialog. Then select from the listbox and accept the default of “1”. The top portion of the ARCH test results shows that the data suggest the presence of ARCH in the residuals:
In addition to serial correlation and ARCH, there is an even more fundamental problem with the above specification since, as the graphs attest, LOG(M1) exhibits a pronounced upward trend, suggesting that we should perform a unit root in this series. The presence of a unit root will indicate the need for further analysis.
We once again display the LOG(M1) series window by clicking on and selecting the LOG(M1) series window from the menu. If the series window for LOG(M1) is not present (if you previously closed the window), you may again open a new window by selecting , entering “log(m1)”, and clicking .
Before computing the test statistic, we will reset the workfile sample to all of the observations by clicking on Quick/Sample... and entering “@all” in the dialog.
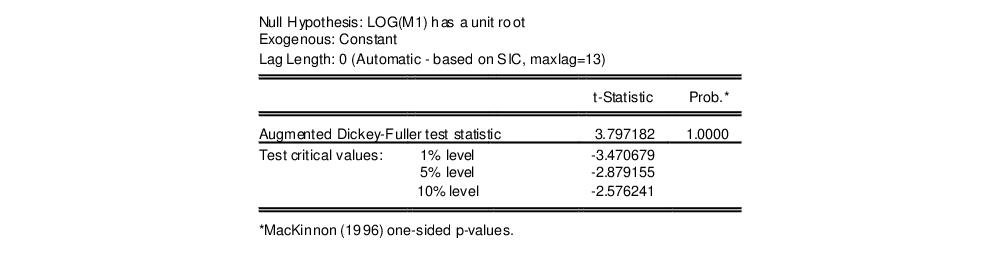
Next, to perform an Augmented Dickey-Fuller (ADF) test for nonstationarity of this series, select and click on to accept the default options. EViews will perform an ADF test and display the test results. The top portion of the output reads:
EViews performs the ADF test statistic with the number of lagged difference terms in the test equation (here, four) determined by automatic selection. The ADF test statistic value has a probability value of 0.9911, providing little evidence that we may reject the null hypothesis of a unit root.
If a unit root were present in our data, we may wish to adopt more sophisticated statistical models. These techniques are discussed in
“Time Series Regression”,
“Vector Autoregression (VAR) Models” which deal with basic time series, cointegrating regression models, and vector error correction specifications, respectively).