EViews Help: Estimating Functional Coefficients Models in EViews

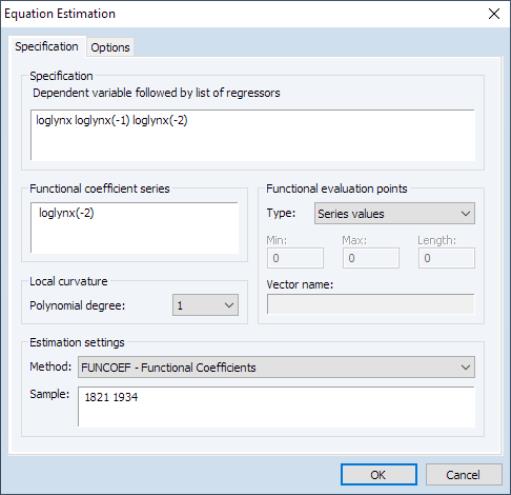
To estimate a functional coefficient model, Quick/Estimate Equation... from the main EViews menu and select FUNCOEF - Functional Coefficients from the main Method dropdown menu near the bottom of the dialog to display the functional coefficients dialog:

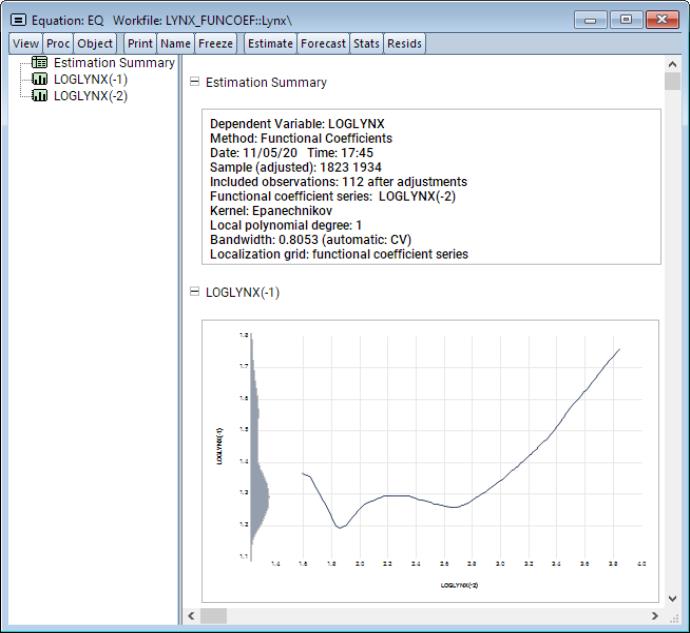
• In the Specification edit field you should enter your dependent variable followed by a list of functional coefficient regressors. Here, LOGLYNX is the dependent variable, and the two lag variables LOGLYNX(-1) and LOGLYNX(-2) will have functional coefficients.

• In the Functional coefficient series variable edit field, you will enter the

variable upon which the functional coefficients depend. Here the coefficients will vary with LOGLYNX(-2).

• In the Local curvature section, the Polynomial Degree dropdown allows you to choose the degree of the regression approximation. For example, local linear regression will set this to 1.

• The Functional evaluation points options group allows you to control the evaluation points for the estimation. The Type dropdown specifies the source of the evaluation points. By default, the values at which we evaluate the functional coefficients are set to the actual data Series values

. If you wish to control the evaluation points, you may select Uniform grid and provide a minimum, maximum, and length, to create the corresponding evenly spaced grid. Alternatively, if the custom grid is stored as a vector in the workfile, select Vector values and enter the name of the vector.

• From the Final bandwidth group Method dropdown, you may select the method for choosing the estimation bandwidth. You may choose between: Rule of thumb, Rule of thumb - robust, Residual squares criterion, Multi Cross-validation (default), Mean square error, Leave one out, Nonparametric AIC, and User-specified. If a User-specified bandwidth is requested, you will be prompted to enter a bandwidth.

• Associated with the automated bandwidth methods are bandwidth search options specifying the Min, Max, Length, Step%, and Stop settings. The first three set the minimum, maximum, and length of the bandwidth grid over which to search for an optimal bandwidth. The last two determine the increment by which to increase the grid value when searching, and how many consecutive failures to improve upon the optimal bandwidth are permitted before the search is terminated. Note here that the search also terminates whenever either the maximum is reached, or the number of bandwidths searched reaches the length specified. Furthermore, when the bandwidth mechanism is Multi Cross-Validation, the number of forecast steps is specified in the m edit field, and the number of sub-series to evaluate may be specified under Q (see “Pilot Bandwidth”).

• Next, the type of kernel used in estimation may be specified in the Kernel type dropdown. You may choose between: Uniform, Triangular, Epanechnikov (default), Biweight, Triweight, and Gaussian. Note that the types are ordered from least to most smooth.

• Lastly, when the estimation bandwidth requires a pilot bandwidth, the latter may be specified Pilot bandwidth group Method dropdown. The options here follow the same principles outlined for the main bandwidth selection method. Since a pilot bandwidth procedure also requires an auxiliary estimation degree, the latter can be specified from the Auxiliary local curvature group by selecting an appropriate value from the Added polynomial degree dropdown. Note here that this auxiliary degree is in addition to the main polynomial degree specified on the Specification tab. In other words, if the main polynomial degree is 1, and the auxiliary polynomial degree is 2, then the pilot polynomial degree will be equal to 3.

Once you have specified your functional coefficients regression specification and set the options, clicking on OK estimates the model and displays results in the form of spool output:

The Equation Summary shows the functional coefficients estimation settings. Below these settings are graphs showing the functional coefficients relationships for each of the regressors.