Detrend each column of a matrix.
Syntax: @coldetrend(m)
m: matrix
Return: matrix
Returns the matrix containing the results from detrending each column of m.
Detrending produces the residuals of the OLS regression of the data in column
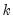
versus an intercept and implicit time trend. For each element of the output matrix
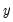
:
where
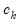
and
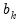
are the intercept and slope coefficients of a regression of the data in column
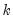
on a constant and time trend. If there are missing values in a column, they are ignored.
Examples
matrix m1 = @mnrnd(50, 4)
matrix m1d = @coldetrend(m1)
detrends each column of M1 and places the results in M1D.
This operation is equivalent to
vector cintercepts = @cintercept(m1)
vector ctrendcs = @ctrendcoef(m1)
matrix m2d = m1 - @kronecker(@ones(m1.@rows), cintercepts.@t) - @kronecker(@range(0, m1.@rows-1), ctrendcs.@t)
where @cintercept and @ctrendcoef are used to compute the coefficients of the column trend regressions.
Cross-references
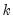 versus an intercept and implicit time trend. For each element of the output matrix
versus an intercept and implicit time trend. For each element of the output matrix 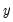 :
: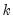 versus an intercept and implicit time trend. For each element of the output matrix
versus an intercept and implicit time trend. For each element of the output matrix 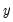 :
: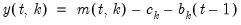
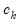 and
and 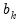 are the intercept and slope coefficients of a regression of the data in column
are the intercept and slope coefficients of a regression of the data in column 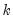 on a constant and time trend. If there are missing values in a column, they are ignored.
on a constant and time trend. If there are missing values in a column, they are ignored.