Cumulative quantiles of a series.
Increasing samples calculation of the quantile value where approximately 100*q percent of the data is less than or equal to the value,
Syntax: @cumquantile(x, q, [s])
x: series
q: number, series
s: (optional) sample string or object
Return: series
• The quantile value
q must satisfy
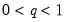
.
• The cumulative quantiles are computed using the Rankit-Cleveland definition of the empirical distribution function: for observation
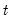
,
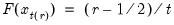
.
To compute the cumulative quantile for observation
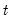
find
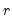
, the smallest rank such that:
where the order statistics
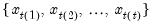
represent data from the beginning of the workfile or sample
s, up to the current observation (
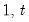
), ordered from low to high. For purposes of computing
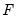
, tied ranks are assumed to take the last tied value.
Then the quantile is computed as
where the interpolating constant is
for
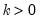
the smallest integer where
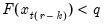
. In the leading case where there are no tied
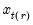
values,
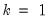
.
This function is panel aware.
Examples
show @cumquantile(@nrnd, 0.975)
generates a linked series that converges in probability to 1.95996... (the 97.5th percentile of the standard normal distribution).
Cross-references
For the backward variant of this function, see
@cumbquantile.
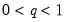 .
.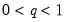 .
.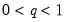 .
.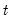 ,
, 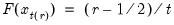 .
.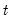 find
find 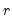 , the smallest rank such that:
, the smallest rank such that: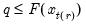
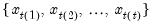 represent data from the beginning of the workfile or sample s, up to the current observation (
represent data from the beginning of the workfile or sample s, up to the current observation (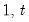 ), ordered from low to high. For purposes of computing
), ordered from low to high. For purposes of computing 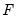 , tied ranks are assumed to take the last tied value.
, tied ranks are assumed to take the last tied value.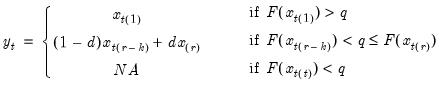
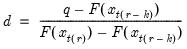
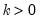 the smallest integer where
the smallest integer where 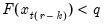 . In the leading case where there are no tied
. In the leading case where there are no tied 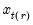 values,
values, 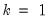 .
.