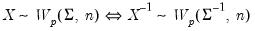X: sym, 

@dwish |

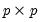
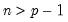
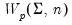 density function for sym values of X, and
density function for sym values of X, and 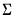 .
.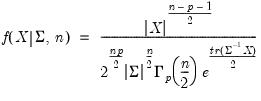
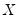 and
and 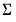 are symmetric
are symmetric 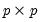 matrices, and
matrices, and 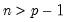 .
. . The forms are distinguished by different suffixes that are applied to the base “@dwish” command and how they change the interpretation of the S matrix argument:
. The forms are distinguished by different suffixes that are applied to the base “@dwish” command and how they change the interpretation of the S matrix argument:@dwish | “” | Supply 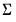 . . |
@dwishc | “c” | Supply the Cholesky decomposition of 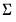 . . This form is more efficient when performing multiple draws from the same distribution (compute the Cholesky once, but sample many times). |
@dwishi | “i” | Supply 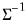 . . This form is more efficient than explicitly inverting 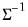 to supply to supply 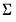 . . |
@dwishic | “ic” | Supply the Cholesky decomposition of 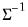 . . This form combines the efficiencies of the Cholesky and inverse forms. |
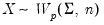 is generally thought of as the accumulated scatter matrix of n random draws from
is generally thought of as the accumulated scatter matrix of n random draws from 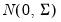 , i.e.,
, i.e., 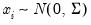 ,
,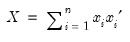 ,
, is a Wishart random variable, then
is a Wishart random variable, then 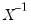 follows an inverse Wishart distribution:
follows an inverse Wishart distribution: