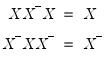Moore-Penrose pseudo-inverse of matrix.
Syntax: @pinverse(m)
m: matrix, sym
Return: matrix, sym
Returns the Moore-Penrose pseudo-inverse of a matrix object or sym.
The pseudo-inverse has the property that both pre-multiplying and post-multiplying the pseudo-inverse by the source matrix returns the source matrix, and that both pre-multiplying and post-multiplying the source matrix by the pseudo-inverse will return the pseudo-inverse.
For matrix
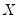
and pseudo-inverse
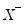
,
Calling the function to produce the pseudo-inverse of a matrix returns a matrix, while the pseudo-inverse of a sym returns a sym. Note that pseudo-inverting a sym is much faster than inverting a matrix.
Examples
matrix m1 = @mnrnd(10, 10)
matrix m1p = @pinverse(m1)
computes the pseudo-inverse of a randomly generated matrix M1.
matrix m2p = @pinverse(@inner(m1))
computes the pseudo-inverse of the PSD inner product of M1.
The following validate the properties of the pseudo-inverse:
matrix diff1 = m1 * m1p * m1 - m1
matrix diff2 = m1p * m1 * m1p - m1p
as both DIFF1 and DIFF2 equal zero.
Cross-references
 and pseudo-inverse
and pseudo-inverse 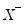 ,
, 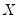 and pseudo-inverse
and pseudo-inverse 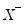 ,
, 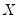 and pseudo-inverse
and pseudo-inverse 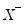 ,
,