Reverse sweep operator.
There are two syntaxes for @rsweep, one for the symmetric, and the other for then non-symmetric operator.
Syntax: @rsweep(s[, n])
s: sym
k: integer
k2: (optional) integer
Return: matrix
Returns the result of applying the symmetric sweep operator to symmetric matrix S at diagonal element k. If k2 is specified, sweeps on all diagonal elements between k and k2, inclusive.
This is merely an alias for @sweep(s, k[, k2]), since the symmetric sweep operator is its own reverse/inverse.
Syntax: @rsweep(m, r, c)
m: matrix, sym
r: integer
c: integer
Return: matrix
Returns the result of applying the reverse non-symmetric sweep operator to general matrix M at element (r, c).
Let
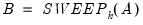
be an application of the symmetric sweep operator. Then,
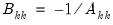
,
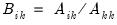
where
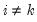
,
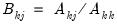
where

, and
where
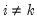
and
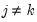
.
Let
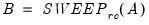
be an application of the non-symmetric sweep operator. Then,
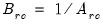
,

where
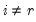
,
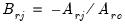
where
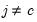
, and
where
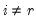
and
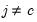
.
Examples
Consider a swept matrix replicating the results of an OLS regression (see @sweep function).
group g y x1 x2 x3
sym usscp = @inner(g)
sym s = @sweep(usscp, 2, 4)
Just as each application of the sweep operator effectively switched the role of a variable from dependent to regressor, each application of the reverse sweep operator switches the role of a variable from regressor back to dependent.
For example, we can remove X1 as a regressor for Y by applying @rsweep to the corresponding diagonal element.
s = @rsweep(s, 2, 2)
We can also verify these results against a standard equation object:
vector beta = @subextract(S, 3, 1, 4, 1) ' Regressor coefficients
scalar ssr = s(1,1) ' Sum of squared residuals
sym invXtX = -@subextract(s, 3, 3)
vector se = @sqrt(ssr * @getmaindiagonal(invXtX) / (@obssmpl - 2)) ' Coefficient standard errors
equation eq.ls(noconst) y x2 x3
Cross-references
Goodnight, James H. (1979). “A Tutorial on the SWEEP Operator,” The American Statistician, 33, 149–158.
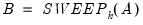 be an application of the symmetric sweep operator. Then,
be an application of the symmetric sweep operator. Then, 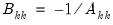 ,
, 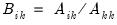 where
where 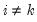 ,
, 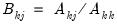 where
where  , and
, and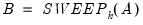 be an application of the symmetric sweep operator. Then,
be an application of the symmetric sweep operator. Then, 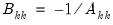 ,
, 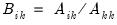 where
where 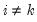 ,
, 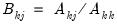 where
where  , and
, and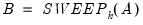 be an application of the symmetric sweep operator. Then,
be an application of the symmetric sweep operator. Then, 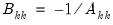 ,
, 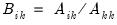 where
where 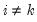 ,
, 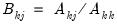 where
where  , and
, and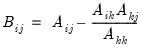
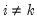 and
and 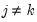 .
.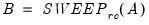 be an application of the non-symmetric sweep operator. Then,
be an application of the non-symmetric sweep operator. Then, 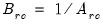 ,
,  where
where 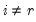 ,
, 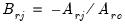 where
where 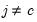 , and
, and
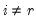 and
and 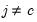 .
.