Definitions
The basic information criteria are given by:
Akaike info criterion (AIC) | |
Schwarz criterion (SC) | |
Hannan-Quinn criterion (HQ) | |
Let
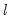
be the value of the log of the likelihood function with the
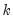
parameters estimated using

observations. The various information criteria are all based on –2 times the average log likelihood function, adjusted by a penalty function.
For factor analysis models, EViews follows convention (Akaike, 1987), re-centering the criteria by subtracting off the value for the saturated model. The resulting factor analysis form of the information criteria are given by:
Akaike info criterion (AIC) | |
Schwarz criterion (SC) | |
Hannan-Quinn criterion (HQ) | |
where

is the discrepancy function, and
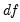
is the number of degrees-of-freedom in the estimated dispersion matrix. Note that EViews scales the Akaike form of the statistic by dividing by
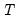
.
In addition to the information criteria described above, there are specialized information criteria that are used in by EViews when computing unit root tests:
Modified AIC (MAIC) | |
Modified SIC (MSIC) | |
Modified Hannan-Quinn (MHQ) | |
where the modification factor
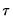
is computed as:
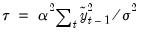 | (60.29) |
for
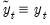
when computing the ADF test equation
(42.25), and for
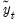
as defined in (
“Autoregressive Spectral Density Estimator”) when estimating the frequency zero spectrum (see Ng and Perron, 2001, for a discussion of the modified information criteria).
Note also that:
• The definitions used by EViews may differ slightly from those used by some authors. For example, Grasa (1989, equation 3.21) does not divide the AIC by
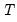
. Other authors omit inessential constants of the Gaussian log likelihood (generally, the terms involving
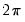
).
While very early versions of EViews reported information criteria that omitted inessential constant terms, the current version of EViews always uses the value of the full likelihood function. All of your equation objects estimated in earlier versions of EViews will automatically be updated to reflect this change. You should, however, keep this fact in mind when comparing results from frozen table objects or printed output from previous versions.
• For systems of equations, where applicable, the information criteria are computed using the full system log likelihood. The log likelihood value is computed assuming a multivariate normal (Gaussian) distribution as:
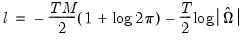 | (60.30) |
where
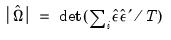 | (60.31) |

is the number of equations. Note that these expressions are only strictly valid when you there are equal numbers of observations for each equation. When your system is unbalanced, EViews replaces these expressions with the appropriate summations.
• The factor analysis forms of the statistics are often quoted in unscaled form, sometimes without adjusting for the saturated model. Most often, if there are discrepancies, multiplying the EViews reported values by
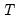
will line up results.
• Many estimation methods, including least squares regression, do not treat the error variance term, sigma, as an estimated coefficient, and as such omit this term from the calculation of

.
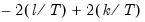
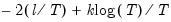

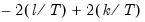
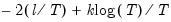

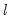 be the value of the log of the likelihood function with the
be the value of the log of the likelihood function with the 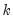 parameters estimated using
parameters estimated using  observations. The various information criteria are all based on –2 times the average log likelihood function, adjusted by a penalty function.
observations. The various information criteria are all based on –2 times the average log likelihood function, adjusted by a penalty function.
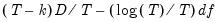
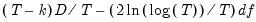
 is the discrepancy function, and
is the discrepancy function, and 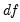 is the number of degrees-of-freedom in the estimated dispersion matrix. Note that EViews scales the Akaike form of the statistic by dividing by
is the number of degrees-of-freedom in the estimated dispersion matrix. Note that EViews scales the Akaike form of the statistic by dividing by 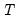 .
.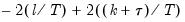
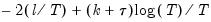
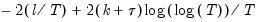
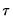 is computed as:
is computed as: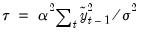
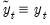 when computing the ADF test equation
(42.25), and for
when computing the ADF test equation
(42.25), and for 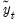 as defined in (
“Autoregressive Spectral Density Estimator”) when estimating the frequency zero spectrum (see Ng and Perron, 2001, for a discussion of the modified information criteria).
as defined in (
“Autoregressive Spectral Density Estimator”) when estimating the frequency zero spectrum (see Ng and Perron, 2001, for a discussion of the modified information criteria). 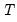 . Other authors omit inessential constants of the Gaussian log likelihood (generally, the terms involving
. Other authors omit inessential constants of the Gaussian log likelihood (generally, the terms involving 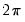 ).
).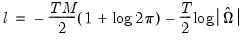
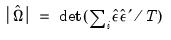
 is the number of equations. Note that these expressions are only strictly valid when you there are equal numbers of observations for each equation. When your system is unbalanced, EViews replaces these expressions with the appropriate summations.
is the number of equations. Note that these expressions are only strictly valid when you there are equal numbers of observations for each equation. When your system is unbalanced, EViews replaces these expressions with the appropriate summations.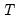 will line up results.
will line up results. .
.