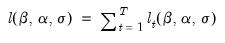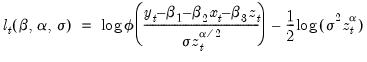Overview
Most of the work in estimating a model using the logl object is in creating the text specification which will be used to evaluate the likelihood function.
If you are familiar with the process of generating series in EViews, you should find it easy to work with the logl specification, since the likelihood specification is merely a list of series assignment statements which are evaluated iteratively during the course of the maximization procedure. All you need to do is write down a set of statements which, when evaluated, will describe a series containing the contributions of each observation to the log likelihood function.
To take a simple example, suppose you believe that your data are generated by the conditional heteroskedasticity regression model:
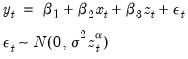 | (41.1) |
where
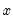
,
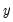
, and
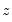
are the observed series (data) and
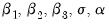
are the parameters of the model. The log likelihood function (the log of the density of the observed data) for a sample of
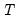
observations can be written as:
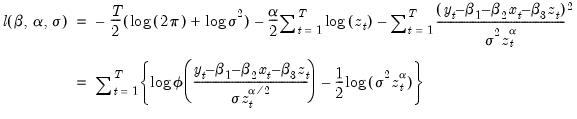 | (41.2) |
where
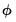
is the standard normal density function.
Note that we can write the log likelihood function as a sum of the log likelihood contributions for each observation
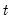
:
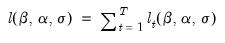 | (41.3) |
where the individual contributions are given by:
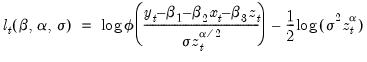 | (41.4) |
Suppose that you know the true parameter values of the model, and you wish to generate a series in EViews which contains the contributions for each observation. To do this, you could assign the known values of the parameters to the elements C(1) to C(5) of the coefficient vector, and then execute the following list of assignment statements as commands or in an EViews program:
series res = y - c(1) - c(2)*x - c(3)*z
series var = c(4) * z^c(5)
series logl1 = log(@dnorm(res/@sqrt(var))) - log(var)/2
The first two statements describe series which will contain intermediate results used in the calculations. The first statement creates the residual series, RES, and the second statement creates the variance series, VAR. The series LOGL1 contains the set of log likelihood contributions for each observation.
Now suppose instead that you do not know the true parameter values of the model, and would like to estimate them from the data. The maximum likelihood estimates of the parameters are defined as the set of parameter values which produce the largest value of the likelihood function evaluated across all the observations in the sample.
The logl object makes finding these maximum likelihood estimates easy. Simply create a new log likelihood object, input the assignment statements above into the logl specification view, then ask EViews to estimate the specification.
In entering the assignment statements, you need only make two minor changes to the text above. First, the series keyword must be removed from the beginning of each line (since the likelihood specification implicitly assumes it is present). Second, an extra line must be added to the specification which identifies the name of the series in which the likelihood contributions will be contained. Thus, you should enter the following into your log likelihood object:
@logl logl1
res = y - c(1) - c(2)*x - c(3)*z
var = c(4) * z^c(5)
logl1 = log(@dnorm(res/@sqrt(var))) - log(var)/2
The first line in the log likelihood specification, @logl logl1, tells EViews that the series LOGL1 should be used to store the likelihood contributions. The remaining lines describe the computation of the intermediate results, and the actual likelihood contributions.
When you tell EViews to estimate the parameters of this model, it will execute the assignment statements in the specification repeatedly for different parameter values, using an iterative algorithm to search for the set of values that maximize the sum of the log likelihood contributions. When EViews can no longer improve the overall likelihood, it will stop iterating and will report final parameter values and estimated standard errors in the estimation output.
The remainder of this chapter discusses the rules for specification, estimation and testing using the likelihood object in greater detail.
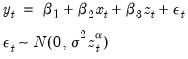
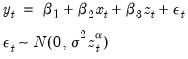
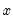 ,
, 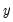 , and
, and 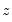 are the observed series (data) and
are the observed series (data) and 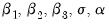 are the parameters of the model. The log likelihood function (the log of the density of the observed data) for a sample of
are the parameters of the model. The log likelihood function (the log of the density of the observed data) for a sample of 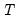 observations can be written as:
observations can be written as: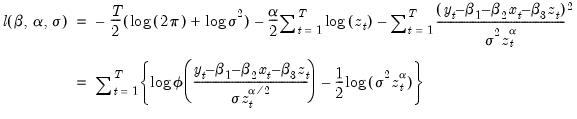
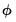 is the standard normal density function.
is the standard normal density function.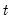 :
: