 | 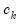 | 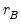 | 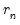 | |
Truncated uniform |  | 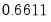 |  | --- |
Bartlett | 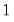 | 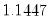 | 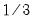 | 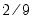 |
Bohman | 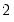 | 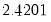 | 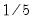 |  |
Daniell | 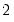 | 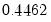 | 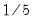 | --- |
Parzen | 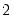 |  | 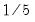 | 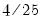 |
Parzen-Riesz | 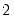 | 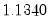 | 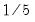 | 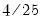 |
Parzen-Geometric | 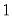 |  | 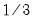 | 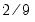 |
Parzen-Cauchy | 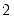 | 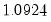 | 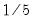 | 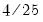 |
Quadratic Spectral |  | 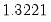 | 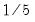 | 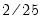 |
Tukey-Hamming | 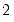 | 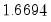 | 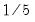 | 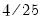 |
Tukey-Hanning | 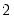 |  | 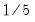 | 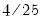 |
Tukey-Parzen | 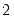 | 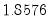 | 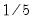 | 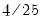 |
 | 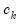 | 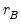 | 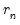 | |
Truncated uniform | 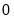 | 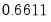 |  | --- |
Bartlett | 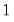 | 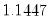 | 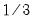 | 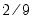 |
Bohman | 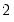 | 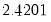 | 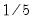 |  |
Daniell | 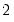 | 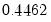 | 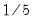 | --- |
Parzen | 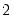 |  | 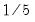 | 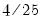 |
Parzen-Riesz | 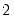 | 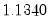 | 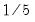 | 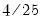 |
Parzen-Geometric | 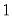 |  | 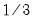 | 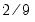 |
Parzen-Cauchy | 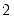 | 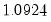 | 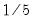 | 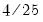 |
Quadratic Spectral |  | 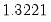 | 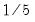 | 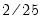 |
Tukey-Hamming | 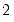 | 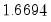 | 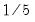 | 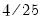 |
Tukey-Hanning | 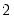 |  | 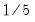 | 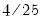 |
Tukey-Parzen | 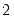 | 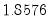 | 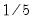 | 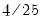 |
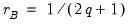 is the optimal rate of increase for the LRCOV kernel bandwidth.
is the optimal rate of increase for the LRCOV kernel bandwidth.  is the optimal rate of increase for the lag selection parameter in the Newey-West (1987) automatic bandwidth selection procedure. The Truncated uniform kernel does not have theoretically proscribed values for
is the optimal rate of increase for the lag selection parameter in the Newey-West (1987) automatic bandwidth selection procedure. The Truncated uniform kernel does not have theoretically proscribed values for 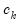 and
and 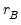 , but Andrews (1991) reports Monte Carlo simulations that suggest that these values work well. The Daniell kernel value for
, but Andrews (1991) reports Monte Carlo simulations that suggest that these values work well. The Daniell kernel value for 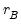 does not follow from the theory since the kernel does not satisfy the conditions of the optimal bandwidth theorems.
does not follow from the theory since the kernel does not satisfy the conditions of the optimal bandwidth theorems.