Function | Name | Description |
@cor(x,y[,s]) | correlation | the correlation between X and Y. |
@cov(x,y[,s]) | covariance | the covariance between X and Y (division by 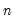 ). ). |
@covp(x,y[,s]) | population covariance | the covariance between X and Y (division by 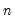 ). ). |
@covs(x,y[,s]) | sample covariance | the covariance between X and Y (division by 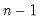 ). ). |
@dupselem(x1[, x2,..., smpl]) | duplicate identification | element IDs enumerating the observations within a duplicate group, as determined by @dupsid. The element IDs for any two observations with the same group ID are distinct. |
@dupsid(x1[, x2,..., smpl]) | duplicate identification | group IDs identifying unique/duplicated observation data, similar to @groupid. The IDs for two observations are identical if and only if the values of series, alphas, or groups s1, s2, etc., are identical for both observations. |
@dupsobs(x1[, x2,..., smpl]) | duplicate identification | number of occurrences of each observation's group ID as would be assigned by @dupsid. An observation containing a unique combination of values among series, alphas, or groups s1, s2, etc., will therefore have the value one, while any duplicated observation will have a value larger than one. |
@gmean(x[,s]) | geometric mean | the geometric mean of X. The geometric mean is calculated as the exponential of the sum of the logs of X. |
@hmean(x[,s]) | harmonic mean | computes the harmonic mean of the values of X. The harmonic mean is calculated as the reciprocal of the mean of the reciprocals of X. |
@imax(x) | maximum index | workfile index of the maximum of the values in X for the current sample. |
@imin(x) | minimum index | workfile index of the maximum of the values in X for the current sample. |
@inner(x,y[,s]) | inner product | the inner product of X and Y. |
@intercept(x[, s]) | intercept | the intercept (or intercepts for panel data) of an OLS regression versus an implicit time trend, as would be used by @detrend. This function is panel aware. |
@kurt(x[,s]) | kurtosis | kurtosis of values in X. |
@mae(x,y[,s]) | mean absolute error | the mean of the absolute value of the difference between X and Y. |
@mape(x,y[,s]) | mean absolute percentage error | 100 multiplied by the mean of the absolute difference between X and Y, divided by Y. |
@max(x[,s]) | maximum | maximum of the values in X. |
@maxes(x,n[,s]) | n-largest numbers | maximum n values in X, arranged largest to smallest, returned in a vector object. Note this function may not be used for series generation. |
@mean(x[,s]) | mean | average of the values in X. |
@median(x[,s]) | median | computes the median of the X (uses the average of middle two observations if the number of observations is even). |
@min(x[,s]) | minimum | minimum of the values in X. |
@mins(x,n[,s]) | n-smallest numbers | minimum n values in X, arranged smallest to largest, returned in a vector object. Note this function may not be used for series generation. |
@mse | mean square error | the mean of the squared difference between X and Y. |
@nas(x[,s]) | number of NAs | the number of missing observations for X in the current sample. |
@pctiles(x[, ties, s]) | percentiles | Similar to @ranks, but returns the percentile of each observation within the series. Equivalent to 100 * @ranks(x, ”a”, ties) / @obs(x). |
@prod(x[,s]) | product | the product of the elements of X (note this function is prone to numerical overflows). |
@obs(x[,s]) | number of observations | the number of non-missing observations for X in the current sample. |
@quantile(x,q[,m,s]) | quantile | the q-th quantile of the series X. m is an optional string argument for specifying the quantile method: “b” (Blom), “r” (Rankit-Cleveland), “o” (Ordinary), “t” (Tukey), “v” (van der Waerden), “g” (Gumbel). The default value is “r”. |
@ranks(x[,o,t,s]) | ranks | the ranking of each observation in X. The order of ranking is set using o: “a” (ascending - default) or “d” (descending). Ties are broken according to the setting of t: “i” (ignore), “f” (first), “l” (last), “a” (average - default), “r” randomize. If you wish to specify tie-handling options, you must also specify the order option (e.g. ‘@ranks(x, “a”, “i”)’). |
@rmse(x,y[,s]) | root mean square error | the square root of the mean of the squared difference between X and Y. |
@skew(x[,s]) | skewness | skewness of values in X. |
@smape(x,y[,s]) | symmetric mean absolute percentage error | 200 multiplied by the mean of the absolute difference between X and Y divided by the sum of the absolute values of X and Y. |
@stdev(x[,s]) | standard deviation | square root of the unbiased sample variance (sum-of-squared residuals divided by 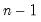 ). ). |
@stdevp(x[,s]) | population standard deviation | square root of the population variance (sum-of-squared residuals divided by  ). ). |
@stdevs(x[,s]) | sample standard deviation | square root of the unbiased sample variance. Note this is the same calculation as @stdev. |
@stdize(x[, smpl]) | standardize (for sample) | Returns a copy of series scaled and translated to have a mean of zero and a sample standard deviation of one. |
@stdizep(x[, smpl]) | standardize (for population) | Returns a copy of series scaled and translated to have a mean of zero and a population standard deviation of one. |
@sum(x[,s]) | sum | the sum of X. |
@sumsq(x[,s]) | sum-of-squares | sum of the squares of X. |
@theil(x,y[,s]) | Theil inequality coefficient | the root mean square error divided by the sum of the square roots of the means of X squared and Y squared. |
@trendcoef(x[, s]) | trend coefficient | the slope of an OLS regression versus an implicit time trend, as would be used by @detrend. This function is panel aware. |
@trmean(x, p[, s]) | trimmed mean | Returns the p-percent trimmed mean, i.e. the mean of after the p-percent largest and smallest values have been removed. |
@var(x[,s]) | variance | variance of the values in X (division by 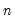 ). ). |
@varp(x[,s]) | population variance | variance of the values in X. Note this is the same calculation as @var. |
@vars(x[,s]) | sample variance | sample variance of the values in X (division by 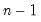 ). ). |