We will work with the standard triangular representation of a regression specification and assume the existence of a single cointegrating vector as in Hansen (1992). Consider a panel structure for the 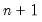 dimensional time series vector process
dimensional time series vector process 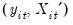 , with cointegrating equation
, with cointegrating equation
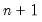 dimensional time series vector process
dimensional time series vector process 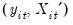 , with cointegrating equation
, with cointegrating equation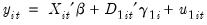
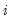 and periods
and periods 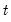 , where
, where 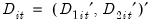 are deterministic trend regressors and the
are deterministic trend regressors and the 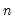 stochastic regressors
stochastic regressors 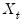 are governed by the system of equations:
are governed by the system of equations:
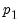 -vector of
-vector of 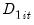 regressors enter into both the cointegrating equation and the regressors equations, while the
regressors enter into both the cointegrating equation and the regressors equations, while the 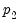 -vector of
-vector of  are deterministic trend regressors which are included in the regressors equations but excluded from the cointegrating equation (see
are deterministic trend regressors which are included in the regressors equations but excluded from the cointegrating equation (see
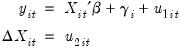
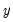 and
and  is assumed to be homogeneous across cross-sections, and that the specification allows for cross-section specific deterministic effects.
is assumed to be homogeneous across cross-sections, and that the specification allows for cross-section specific deterministic effects. 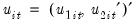 are strictly stationary and ergodic with zero mean, contemporaneous covariance matrix
are strictly stationary and ergodic with zero mean, contemporaneous covariance matrix 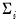 , one-sided long-run covariance matrix
, one-sided long-run covariance matrix 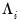 , and long-run covariance matrix
, and long-run covariance matrix 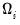 , each of which we partition conformably with
, each of which we partition conformably with 
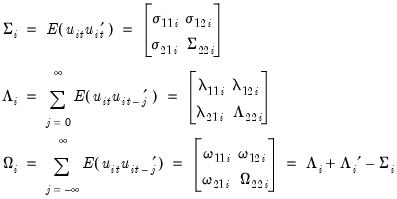
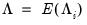 , and
, and 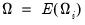 .
.  using extensions of single-equation FMOLS and DOLS methods. There are different variants for each of the estimators depending on the assumptions that one wishes to make about the long-run covariances and how one wishes to use the panel structure of the data.
using extensions of single-equation FMOLS and DOLS methods. There are different variants for each of the estimators depending on the assumptions that one wishes to make about the long-run covariances and how one wishes to use the panel structure of the data.