Quantile Regression
While the great majority of regression models are concerned with analyzing the conditional mean of a dependent variable, there is increasing interest in methods of modeling other aspects of the conditional distribution. One increasingly popular approach, quantile regression, models the quantiles of the dependent variable given a set of conditioning variables.
As originally proposed by Koenker and Bassett (1978), quantile regression provides estimates of the linear relationship between regressors
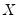
and a specified quantile of the dependent variable
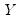
. One important special case of quantile regression is the least absolute deviations (LAD) estimator, which corresponds to fitting the conditional median of the response variable.
Quantile regression permits a more complete description of the conditional distribution than conditional mean analysis alone, allowing us, for example, to describe how the median, or perhaps the 10th or 95th percentile of the response variable, are affected by regressor variables. Moreover, since the quantile regression approach does not require strong distributional assumptions, it offers a robust method of modeling these relationships.
The remainder of this section describes the basics of performing quantile regression in EViews. We begin with a walkthrough showing how to estimate a quantile regression specification and describe the output from the procedure. Next we examine the various views and procedures that one may perform using an estimated quantile regression equation. Lastly, we provide background information on the quantile regression model.
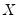 and a specified quantile of the dependent variable
and a specified quantile of the dependent variable 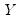 . One important special case of quantile regression is the least absolute deviations (LAD) estimator, which corresponds to fitting the conditional median of the response variable.
. One important special case of quantile regression is the least absolute deviations (LAD) estimator, which corresponds to fitting the conditional median of the response variable.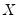 and a specified quantile of the dependent variable
and a specified quantile of the dependent variable 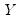 . One important special case of quantile regression is the least absolute deviations (LAD) estimator, which corresponds to fitting the conditional median of the response variable.
. One important special case of quantile regression is the least absolute deviations (LAD) estimator, which corresponds to fitting the conditional median of the response variable.