Estimate generalized autoregressive conditional heteroskedasticity (GARCH) models.
Syntax
arch(p,q,options) y [x1 x2 x3] [@ p1 p2 [@ t1 t2]]
arch(p,q,options) y=expression [@ p1 p2 [@ t1 t2]]
The first two options specify the order of the GARCH model:
• The arch estimation method specifies a GARCH(p, q) model with p ARCH terms and q GARCH terms. Note the order of the arguments in which the ARCH and GARCH terms are entered.
The maximum value for
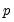
or
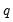
is 9; values above will be set to 9. The minimum value for
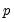
is 1. The minimum value for
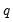
is 0. If either
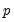
or
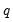
is not specified, EViews will assume a corresponding order of 1. Thus, a GARCH(1, 1) is assumed by default.
• For CGARCH, FIEGARCH and MIDAS-GARCH models, EViews only estimates (1,1) models. For these specifications,
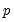
and
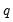
options should not be specified, and if provided, will be ignored.
After the “ARCH” keyword and options, specify the dependent variable followed by a list of regressors in the mean equation.
• By default, only the intercept is included in the conditional variance equation. If you wish to specify variance regressors, list them after the mean equation using an “@”-sign to separate the mean from the variance equation.
• When estimating component ARCH models, you may specify exogenous variance regressors for both the permanent and transitory components. After the mean equation regressors, first list the regressors for the permanent component, followed by an “@”-sign, then the regressors for the transitory component. A constant term is always included as a permanent component regressor.
• For MIDAS-GARCH models, the low-frequency permanent component regressor are entered after the mean equation regressors and an “@”-sign. The regressor should be specified as pagename\seriesname.
Options
Type Options
The default is to estimate a standard GARCH model. You may specify one of the followings keywords to estimate a different model:
egarch | Exponential GARCH. |
parch[=arg] | Power ARCH. If the optional arg is provided, the power parameter will be set to that value, otherwise the power parameter will be estimated. |
cgarch | Component (permanent and transitory) ARCH. |
figarch | Fractional GARCH (FIGARCH). |
fiegarch | Fractional Exponential GARCH (FIEGARCH(1,1)). |
midas | MIDAS GARCH(1,1) |
General Options
thrsh | For Component GARCH models, include a threshold term. |
thrsh=integer (default=0) | Number of threshold terms for GARCH models. The maximum number of terms allowed is 9. |
vt | Variance target of the constant term for GARCH models. (May not be used with integrated specifications.) |
integrated | Restrict GARCH model to be integrated, i.e. IGARCH. (May not be used with variance targeting.) |
asy=integer (default=1) | Number of asymmetric terms in Power ARCH or EGARCH models. The maximum number of terms allowed is 9. |
trunclag=integer (default=1000) | Number of terms in the expansion approximation for FIGARCH and FIEGARCH models. |
archm=arg | ARCH-M (ARCH in mean) specification with the conditional standard deviation (“archm=sd”), the conditional variance (“archm=var”), or the log of the conditional variance (“archm= log”) entered as a regressor in the mean equation. |
tdist [=number] | Estimate the model assuming that the residuals follow a conditional Student’s t-distribution (the default is the conditional normal distribution). Providing the optional number greater than two will fix the degrees of freedom to that value. If the argument is not provided, the degrees of freedom will be estimated. |
ged [=number] | Estimate the model assuming that the residuals follow a conditional GED (the default is the conditional normal distribution). Providing a positive value for the optional argument will fix the GED parameter. If the argument is not provided, the parameter will be estimated. |
z | Turn of backcasting for both initial MA innovations and initial variances. |
backcast=n | Backcast weight to calculate value used as the presample conditional variance. Weight needs to be greater than 0 and less than or equal to 1; the default value is 0.7. Note that a weight of 1 is equivalent to no backcasting, i.e. using the unconditional residual variance as the presample conditional variance. |
optmethod = arg | Optimization method: “bfgs” (BFGS); “newton” (Newton-Raphson), “opg” or “bhhh” (OPG or BHHH), “legacy” (EViews legacy). “bfgs” is the default for new equations. |
optstep = arg | Step method: “marquardt” (Marquardt - default); “dogleg” (Dogleg); “linesearch” (Line search). (Applicable when “optmethod=bfgs”, “optmethod=newton” or “optmethod=opg”.) |
b | Use Berndt-Hall-Hall-Hausman (BHHH) as maximization algorithm. The default is Marquardt. (Applicable when “optmethod=legacy”.) |
cov=arg | Covariance method: “ordinary” (default method based on inverse of the estimated information matrix), “huber” or “white” (Huber-White sandwich method), “bollerslev” (Bollerslev-Wooldridge method). |
covinfo = arg | Information matrix method: “opg” (OPG); “hessian” (observed Hessian), “ (Applicable when non-legacy “optmethod=” with “cov=ordinary”.) |
h | Bollerslev-Wooldridge robust quasi-maximum likelihood (QML) covariance/standard errors. (Applicable for “optmethod=legacy” when estimating assuming normal errors.) |
m=integer | Set maximum number of iterations. |
c=scalar | Set convergence criterion. The criterion is based upon the maximum of the percentage changes in the scaled coefficients. |
s | Use the current coefficient values in “C” as starting values (see also
param). |
s=number | Specify a number between zero and one to determine starting values as a fraction of preliminary LS estimates (out of range values are set to “s=1”). |
numericderiv / ‑numericderiv | [Do / do not] use numeric derivatives only. If omitted, EViews will follow the global default. |
fastderiv / ‑fastderiv | [Do / do not] use fast derivative computation. If omitted, EViews will follow the global default. Available only for legacy estimation (“optmeth=legacy”). |
showopts / ‑showopts | [Do / do not] display the starting coefficient values and estimation options in the estimation output. |
coef=arg | Specify the name of the coefficient vector (if specified by list); the default behavior is to use the “C” coefficient vector. |
prompt | Force the dialog to appear from within a program. |
p | Print estimation results. |
MIDAS Options
lag=arg | Specify the number of lags of the low frequency regressor to include. Default value is 32. |
beta=arg | Beta function restriction: none (“none”), trend coefficient equals 1 (“trend”), endpoints coefficient equals 0 (“end-point”), both trend and endpoints restriction (“both”). For use when “midwgt=beta”. The default is “beta=none”. |
thrsh | Include a threshold term. |
optmethod=arg | Optimization method for nonlinear estimation: “bfgs” (BFGS); “newton” Newton-Raphson), “opg”, “bhhh” (OPG or BHHH), or “hybrid” (initial BHHH followed by BFGS). Hybrid is the default method. |
optstep=arg | Step method for nonlinear estimation: “marquardt” (Marquardt); “dogleg” (Dogleg); “linesearch” (Line search). Marquardt is the default method. |
cov=arg | Covariance method for nonlinear models: “ordinary” (default method based on inverse of the estimated information matrix), “huber” or “white” (Huber-White sandwich). |
covinfo=arg | Information matrix method for nonlinear models: “opg” (OPG); “hessian” (observed Hessian). |
nodf | Do not perform degree of freedom corrections in computing coefficient covariance matrix. The default is to use degree of freedom corrections. |
m=integer | Set maximum number of iterations. |
c=scalar | Set convergence criterion. The criterion is based upon the maximum of the percentage changes in the scaled coefficients. The criterion will be set to the nearest value between 1e-24 and 0.2. |
s | Use the current coefficient values in estimator coefficient vector as starting values in nonlinear estimation. If the “s=number” or “s” options are not used, EViews will use random starting values. |
s=number | Determine starting values for nonlinear estimation. Specify a number between zero and oSpecify the number of lags of the low frequency regressor to include. Default value is 32.ne representing the fraction of preliminary EViews chosen values. Note that out of range values are set to “s=1”. Specifying “s=0” initializes coefficients to zero. If the “s=number” or “s” options are not used, EViews will use random starting values. |
seed=positive_integer from 0 to 2,147,483,647 | Seed the random number generator used in random starting values. If not specified, EViews will seed random number generator with a single integer draw from the default global random number generator. |
showopts/-showopts | [Do / do not] display the starting coefficient values and estimation options in the estimation output. |
coef=arg | Specify the name of the coefficient vector; the default behavior is to use the “C” coefficient vector. |
prompt | Force the dialog to appear from within a program. |
p | Print estimation results. |
Examples
arch(4, 0, m=1000, cov=bollerslev) sp500 c
estimates an ARCH(4) model with a mean equation consisting of the series SP500 regressed on a constant. The procedure will perform up to 1000 iterations, and will report Bollerslev-Wooldridge robust QML standard errors upon completion.
The commands:
c = 0.1
arch(thrsh=1, s, mean=var) @pch(nys) c ar(1)
estimate a TARCH(1, 1)-in-mean specification with the mean equation relating the percent change of NYS to a constant, an AR term of order 1, and a conditional variance (GARCH) term. The first line sets the default coefficient vector to 0.1, and the “s” option uses these values as coefficient starting values.
The command:
arch(1, 2, asy=0, parch=1.5, ged=1.2) dlog(ibm)=c(1)+c(2)* dlog(sp500) @ r
estimates a symmetric Power ARCH(2, 1) (autoregressive GARCH of order 2, and moving average ARCH of order 1) model with GED errors. The power of model is fixed at 1.5 and the GED parameter is fixed at 1.2. The mean equation consists of the first log difference of IBM regressed on a constant and the first log difference of SP500. The conditional variance equation includes an exogenous regressor R.
Cross-references
See
“ARCH and GARCH Estimation” for a discussion of ARCH models.
See
Equation::arch for the equivalent object command.
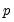 or
or 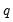 is 9; values above will be set to 9. The minimum value for
is 9; values above will be set to 9. The minimum value for 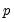 is 1. The minimum value for
is 1. The minimum value for 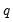 is 0. If either
is 0. If either 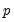 or
or 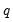 is not specified, EViews will assume a corresponding order of 1. Thus, a GARCH(1, 1) is assumed by default.
is not specified, EViews will assume a corresponding order of 1. Thus, a GARCH(1, 1) is assumed by default. 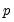 or
or 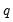 is 9; values above will be set to 9. The minimum value for
is 9; values above will be set to 9. The minimum value for 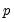 is 1. The minimum value for
is 1. The minimum value for 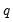 is 0. If either
is 0. If either 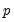 or
or 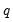 is not specified, EViews will assume a corresponding order of 1. Thus, a GARCH(1, 1) is assumed by default.
is not specified, EViews will assume a corresponding order of 1. Thus, a GARCH(1, 1) is assumed by default. 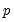 and
and 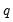 options should not be specified, and if provided, will be ignored.
options should not be specified, and if provided, will be ignored.