Cross-validation Settings
We may use cross-validation model selection techniques to identify a preferred value of
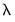
from the path.
Cross-validation involves partitioning the data into training and test sets, estimating the
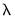
path using the training set, and using the coefficients and the test set to compute evaluation statistics. Some cross-validation methods involve only a single partition, but others produce multiple training and test set partitions.
To specify a cross-validation procedure you must specify both a cross-validation method, and a cross-validation statistic.
Methods
K-Fold
In K-fold cross-validation, the dataset is randomly divided into
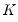
(roughly) evenly sized groups (“folds”). One fold is held out as the test set while the remaining
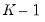
folds are combined into a training set. The model is estimated (“trained”) using the training set and the selection statistic is computed using the observations in the corresponding test set. This training and test step is repeated, with each fold acting as the test set. The selection statistics are averaged over the
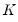
values to obtain a final value.
The number of folds
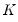
is specified in the edit field.
The randomization procedure is governed by the specified and the random fields. You may the leave the field blank, in which case EViews will use the clock to obtain a seed at the time of estimation, or you may provide an integer from 0 to 2,147,483,647.
Simple Split
In simple split cross-validation, the dataset is divided into a training and test set. A pre-test gap allows for additional separation (oftentimes temporal) between the training and the corresponding test samples.
The model is estimated for the observation in the training set and the selection statistic is computed using the test set.
The simple split method is parameterized using the parameter
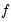
, where the training set is the first
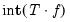
set of observations, the of
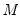
, and the test set is comprised of the remaining
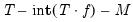
observations.
Monte Carlo
Monte Carlo cross-validation repeatedly splits the sample into a random training set of
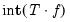
observations, and a test set containing the remaining
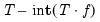
observations.
Monte Carlo cross-validation can be thought of as a repeated simple split computation on randomly ordered data. Estimation and evaluation of the selection statistic are computed using each of the training and corresponding test sets, and the results are averaged to obtain a final selection statistic value.
The training/test split is parameterized using the parameter
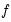
. The number of Monte Carlo random splits is specified in the edit field.
The randomization procedure is governed by the specified and the random fields. You may the leave the field blank, in which case EViews will use the clock to obtain a seed at the time of estimation, or you may provide an integer from 0 to 2,147,483,647.
Leave-One-Out
In Leave-One-Out cross-validation, a single observation is held out as a test set, and the remaining
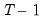
observations are combined into a training set. This procedure is repeated
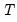
times, with each observation acting once as the test set. The resulting statistics are averaged to obtain a final selection statistic value.
Since a separate model is estimated for each observation in the sample, Leave-One-Out cross-validation is typically employed in settings with relatively small numbers of observations.
Note that Leave-One-Out cross-validation is equivalent to K-Fold cross-validation with the number of folds equal to the number of observations.
Leave-P-Out
In Leave-P-Out cross-validation,
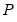
observations are held out as a test set, and the remaining
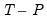
observations are combined into a training set. This procedure is repeated for all distinct sets of
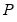
observations in the original sample. The resulting statistics are averaged to obtain a final selection statistic value.
Since the number of models to estimate increases combinatorially with the sample size, Leave-P-Out cross-validation is typically employed in settings with relatively small numbers of observations. We strongly urge caution in using this method even with moderate numbers of observations and
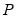
.
The number of leave-out observations
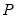
is specified in the edit field.
Rolling Window
The Rolling Window cross-validation method is a time-series oriented approach in which the full sample is divided into non-overlapping windows, and each window in turn divided into a training sample, followed by pre-test gap and a fixed number of test sample observations.
Central to this rolling window approach is a maintaining of all temporal relationships, with all observations ordered sequentially with respect to time, and with the test sample following the training sample.
The pre-test gap allows for additional temporal separation between the training and the corresponding test samples, and the post-test gap provides separation between a test sample and the subsequent training sample.
To specify your settings, fill in the edit field, then specify the number of and, and enter the test sample size in the edit field. The size of the training samples will be determined from the number of observations and the remaining settings.
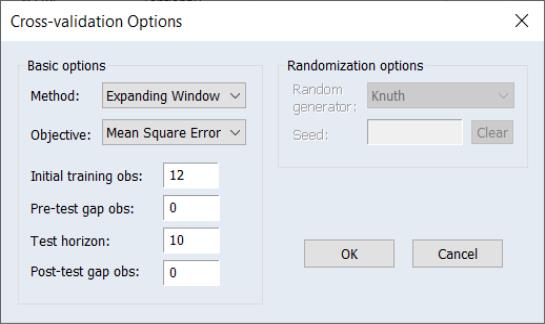
Expanding Window
The Expanding Window cross-validation method is a time-series oriented approach in which we start with an initial training sample, a pre-test gap, and a fixed number of observations in a test sample.
Subsequent cross-validation samples are obtained by expanding the training sample to include the previous employed observations along with a post-test gap, and repeating the training and test procedures.
All temporal relationships are maintained with this approach, with all observations ordered sequentially with respect to time, and with the test sample following the training sample.
You should enter the size of the initial training sample in the edit field, then specify the number of and, and enter the test sample size in the edit field.
Fit Statistics
Given estimation using a cross-validation training sample, we evaluate a measure of fit for the corresponding test sample. EViews offers several different choices for the cross-validation fit statistic. Suppose that we define the fitted value obtained using the coefficients
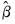
from the training sample estimates:
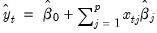 | (37.15) |
Then the fit statistics are defined for the
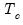
observations in the test sample as:
• (MSE)
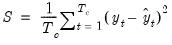 | (37.16) |
•
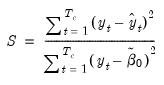 | (37.17) |
where
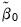
is the test sample mean if the model includes an intercept, and
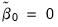
if it does not.
• (MAE – Mean absolute error)
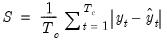 | (37.18) |
• (MAPE – Mean absolute percentage error)
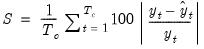 | (37.19) |
Note that cases where
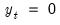
are removed from the computation and
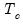
is adjusted accordingly.
• (SMAPE – Symmetric mean absolute percentage error)
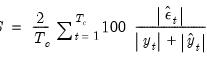 | (37.20) |
Note that cases where
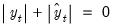
are removed from the computation and
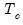
is adjusted accordingly.
If a cross-validation method produces only a single training and test set, the cross-validation statistic is the single value of
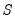
.
If the cross-validation method produces multiple training and test sets, there will be multiple sets of evaluation statistics, one for each training-test set pair. The cross-validation statistic will be the average value of the
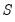
. Further we may compute the standard deviation of the mean of
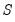
which may be used to provide additional guidance in selecting an optimal
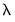
.
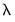 from the path.
from the path.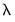 from the path.
from the path.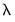 from the path.
from the path.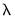 path using the training set, and using the coefficients and the test set to compute evaluation statistics. Some cross-validation methods involve only a single partition, but others produce multiple training and test set partitions.
path using the training set, and using the coefficients and the test set to compute evaluation statistics. Some cross-validation methods involve only a single partition, but others produce multiple training and test set partitions.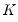 (roughly) evenly sized groups (“folds”). One fold is held out as the test set while the remaining
(roughly) evenly sized groups (“folds”). One fold is held out as the test set while the remaining 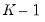 folds are combined into a training set. The model is estimated (“trained”) using the training set and the selection statistic is computed using the observations in the corresponding test set. This training and test step is repeated, with each fold acting as the test set. The selection statistics are averaged over the
folds are combined into a training set. The model is estimated (“trained”) using the training set and the selection statistic is computed using the observations in the corresponding test set. This training and test step is repeated, with each fold acting as the test set. The selection statistics are averaged over the 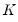 values to obtain a final value.
values to obtain a final value.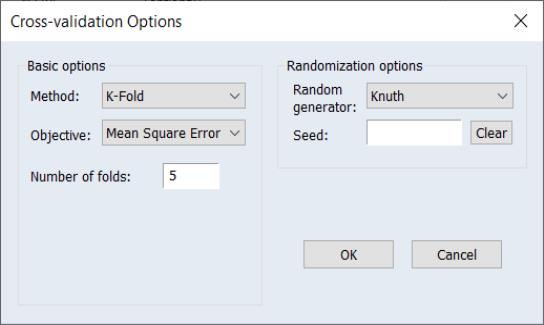
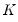 is specified in the Number of folds edit field.
is specified in the Number of folds edit field. 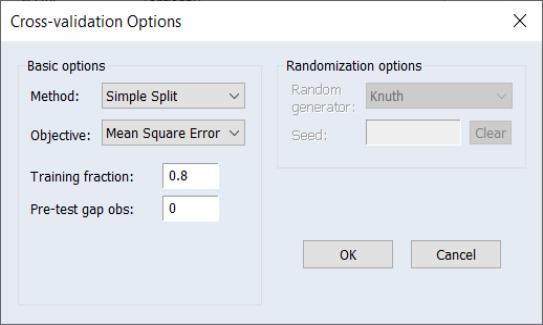
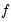 , where the training set is the first
, where the training set is the first 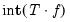 set of observations, the Pre-test gap obs of
set of observations, the Pre-test gap obs of 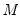 , and the test set is comprised of the remaining
, and the test set is comprised of the remaining 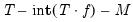 observations.
observations.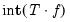 observations, and a test set containing the remaining
observations, and a test set containing the remaining 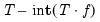 observations.
observations. 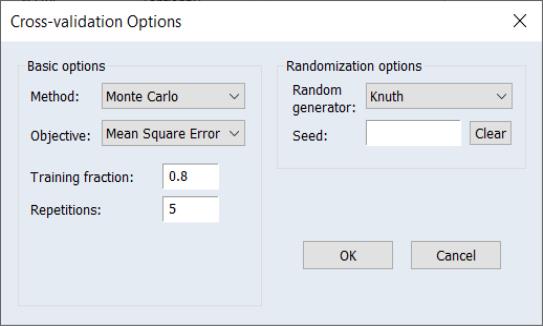
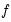 . The number of Monte Carlo random splits is specified in the Repetitions edit field.
. The number of Monte Carlo random splits is specified in the Repetitions edit field. 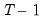 observations are combined into a training set. This procedure is repeated
observations are combined into a training set. This procedure is repeated 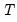 times, with each observation acting once as the test set. The resulting statistics are averaged to obtain a final selection statistic value.
times, with each observation acting once as the test set. The resulting statistics are averaged to obtain a final selection statistic value.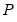 observations are held out as a test set, and the remaining
observations are held out as a test set, and the remaining 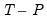 observations are combined into a training set. This procedure is repeated for all distinct sets of
observations are combined into a training set. This procedure is repeated for all distinct sets of 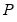 observations in the original sample. The resulting statistics are averaged to obtain a final selection statistic value.
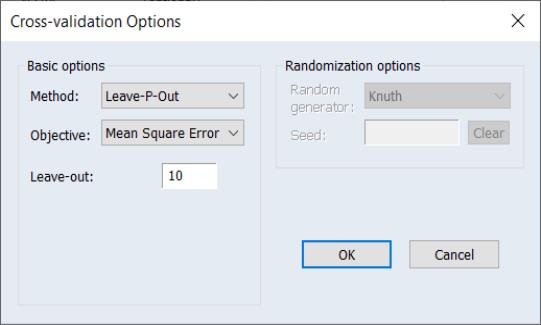
observations in the original sample. The resulting statistics are averaged to obtain a final selection statistic value.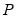 .
.
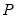 is specified in the Leave-out edit field.
is specified in the Leave-out edit field. 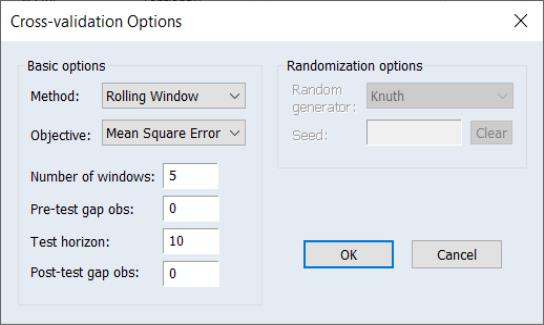
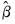 from the training sample estimates:
from the training sample estimates: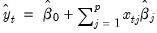
 observations in the test sample as:
observations in the test sample as:
 is the test sample mean if the model includes an intercept, and
is the test sample mean if the model includes an intercept, and 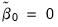 if it does not.
if it does not.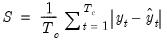
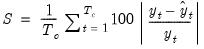
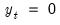 are removed from the computation and
are removed from the computation and 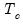 is adjusted accordingly.
is adjusted accordingly.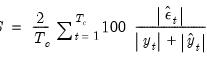
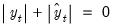 are removed from the computation and
are removed from the computation and 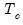 is adjusted accordingly.
is adjusted accordingly.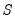 .
.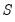 . Further we may compute the standard deviation of the mean of
. Further we may compute the standard deviation of the mean of 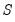 which may be used to provide additional guidance in selecting an optimal
which may be used to provide additional guidance in selecting an optimal 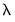 .
.