Perform Wald test of equality of slope coefficients across multiple quantile regression estimates. The equality test restrictions are of the form:
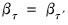
for the slope coefficients

.
Syntax
eq_name.qrslope(options) [arg] [@coefs coeflist]
where arg is a optional list containing the quantile values (specified using numbers, scalar objects, or vectors) for which you wish to compute estimates, and optionally the @coefs keyword followed by a coeflist of the subset of coefficients to display.
• If arg is not specified, EViews will perform tests for the existing equation and coefficients for equations estimated at a set of equally spaced quantiles as specified by the “n=” option. If “n=” is not specified, the default is to display results for the quartiles (.25, .75).
• If arg is specified, EViews will perform results for the original equation along with tests including coefficients for equations estimated at the specified quantiles.
• If a coeflist is not provided, all of the slope coefficients will be employed in the test.
You may specify a maximum of 1000 total coefficients (number of coefficients in the equation specification times the number of quantiles) and a maximum of 500 quantiles in the test.
All estimation will be performed using the settings from the original equation.
Options
n=arg (default=4) | Number of quantiles for process estimates. |
quantout=name | Save vector containing test quantile values. |
coefout=name | Save matrix containing test coefficient estimates. Each column of the matrix corresponds to a different quantile matching the corresponding quantile in “quantout=”. To match the covariance matrix given in “covout=” you should take the @vec of the coefficient matrix. |
covout=name | Save symmetric matrix containing covariance matrix for the vector set of coefficient estimates. |
prompt | Force the dialog to appear from within a program. |
p | Print output from the test. |
Examples
equation eq1.qreg log(y) c log(x)
eq1.qrslope
estimates a quantile (median) regression of LOG(Y) on a constant and LOG(X), and tests for the equality of the coefficients of LOG(X) for all three of the quartiles.
Similarly,
equation eq1.qreg(quant=.4) log(y) c log(x)
eq1.qrslope(coefcout=cout)
tests for equality of the LOG(X) coefficient estimated at {.25, .4, .5, .75}, and saves the coefficient matrix to COUT. Both
eq1.qrslope(coefout=count, n=10)
eq1.qrslope(coefout=cout) .1 .2 .3 .4 .5 .6 .7 .8 .9
perform the Wald test for equality of the slope coefficient across all of the deciles, as does the equivalent
vector v1(9)
v1.fill .1,.2,.3,.4,.5,.6,.7,.8,.9
eq1.qrslope v1
Cross-references
See
“Slope Equality Test” for a discussion of the slope equality test.
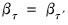 for the slope coefficients
for the slope coefficients  .
.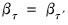 for the slope coefficients
for the slope coefficients  .
.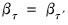 for the slope coefficients
for the slope coefficients  .
.