Gradients
EViews provides you with the ability to examine and work with the gradients of the objective function for a variety of estimation objects. Examining these gradients can provide useful information for evaluating the behavior of your nonlinear estimation routine, or can be used as the basis of various tests of specification.
Since EViews provides a variety of estimation methods and techniques, the notion of a gradient is a bit difficult to describe in casual terms. EViews will generally report the values of the first-order conditions used in estimation. To take the simplest example, ordinary least squares minimizes the sum-of-squared residuals:
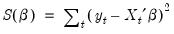 | (60.24) |
The first-order conditions for this objective function are obtained by differentiating with respect to

, yielding
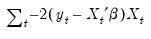 | (60.25) |
EViews allows you to examine both the sum and the corresponding average, as well as the value for each of the individual observations. Furthermore, you can save the individual values in series for subsequent analysis.
The individual gradient computations are summarized in the following table:
Least squares | |
Weighted least squares | |
Two-stage least squares | |
Weighted two-stage least squares | |
Maximum likelihood | |
where

and
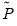
are the projection matrices corresponding to the expressions for the estimators in
“Instrumental Variables and GMM”, and
is the log likelihood contribution function.
Note that the expressions for the regression gradients are adjusted accordingly in the presence of ARMA error terms.
Gradient Summary
To view the summary of the gradients, select , or . EViews will display a summary table showing the sum, mean, and Newton direction associated with the gradients. Here is an example table from a nonlinear least squares estimation equation:
There are several things to note about this table. The first line of the table indicates that the gradients have been computed at estimated parameters. If you ask for a gradient view for an estimation object that has not been successfully estimated, EViews will compute the gradients at the current parameter values and will note this in the table. This behavior allows you to diagnose unsuccessful estimation problems using the gradient values.
Second, you will note that EViews informs you that the gradients were computed using analytic derivatives. EViews will also inform you if the specification is linear, if the derivatives were computed numerically, or if EViews used a mixture of analytic and numeric techniques. We remind you that all MA coefficient derivatives are computed numerically.
Lastly, there is a table showing the sum and mean of the gradients as well as a column labeled “Newton Dir.”. The column reports the non-Marquardt adjusted Newton direction used in first-derivative iterative estimation procedures (see
“First Derivative Methods”).
In the example above, all of the values are “close” to zero. While one might expect these values always to be close to zero when evaluated at the estimated parameters, there are a number of reasons why this will not always be the case. First, note that the sum and mean values are highly scale variant so that changes in the scale of the dependent and independent variables may lead to marked changes in these values. Second, you should bear in mind that while the Newton direction is related to the terms used in the optimization procedures, EViews’ test for convergence does not directly use the Newton direction. Third, some of the iteration options for system estimation do not iterate coefficients or weights fully to convergence. Lastly, you should note that the values of these gradients are sensitive to the accuracy of any numeric differentiation.
Gradient Table and Graph
There are a number of situations in which you may wish to examine the individual contributions to the gradient vector. For example, one common source of singularity in nonlinear estimation is the presence of very small combined with very large gradients at a given set of coefficient values.
EViews allows you to examine your gradients in two ways: as a spreadsheet of values, or as line graphs, with each set of coefficient gradients plotted in a separate graph. Using these tools, you can examine your data for observations with outlier values for the gradients.
Gradient Series
You can save the individual gradient values in series using the procedure. EViews will create a new group containing series with names of the form GRAD## where ## is the next available name.
Note that when you store the gradients, EViews will fill the series for the full workfile range. If you view the series, make sure to set the workfile sample to the sample used in estimation if you want to reproduce the table displayed in the gradient views.
Application to LM Tests
The gradient series are perhaps most useful for carrying out Lagrange multiplier tests for nonlinear models by running what is known as artificial regressions (Davidson and MacKinnon 1993, Chapter 6). A generic artificial regression for hypothesis testing takes the form of regressing:
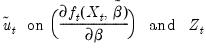 | (60.26) |
where
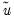
are the estimated residuals under the restricted (null) model, and
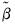
are the estimated coefficients. The
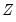
are a set of “misspecification indicators” which correspond to departures from the null hypothesis.
An example program (“GALLANT2.PRG”) for performing an LM auxiliary regression test is provided in your EViews installation directory.
Gradient Availability
The gradient views are currently available for the equation, logl, sspace and system objects. The views are not, however, currently available for equations estimated by GMM or ARMA equations specified by expression.
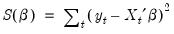
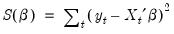
 , yielding
, yielding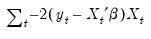
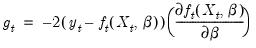

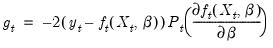

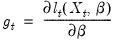
 and
and 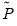 are the projection matrices corresponding to the expressions for the estimators in
“Instrumental Variables and GMM”, and
are the projection matrices corresponding to the expressions for the estimators in
“Instrumental Variables and GMM”, and 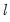 is the log likelihood contribution function.
is the log likelihood contribution function.
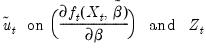
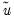 are the estimated residuals under the restricted (null) model, and
are the estimated residuals under the restricted (null) model, and 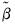 are the estimated coefficients. The
are the estimated coefficients. The 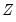 are a set of “misspecification indicators” which correspond to departures from the null hypothesis.
are a set of “misspecification indicators” which correspond to departures from the null hypothesis.