The default standard errors are obtained by taking the inverse of the estimated information matrix. If you estimate your equation using a Newton-Raphson or Quadratic Hill Climbing method, EViews will use the inverse of the Hessian, 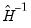 , to form your coefficient covariance estimate. If you employ BHHH, the coefficient covariance will be estimated using the inverse of the outer product of the scores
, to form your coefficient covariance estimate. If you employ BHHH, the coefficient covariance will be estimated using the inverse of the outer product of the scores 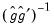 , where
, where 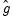 and
and 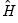 are the gradient (or score) and Hessian of the log likelihood evaluated at the ML estimates.
are the gradient (or score) and Hessian of the log likelihood evaluated at the ML estimates.
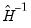 , to form your coefficient covariance estimate. If you employ BHHH, the coefficient covariance will be estimated using the inverse of the outer product of the scores
, to form your coefficient covariance estimate. If you employ BHHH, the coefficient covariance will be estimated using the inverse of the outer product of the scores 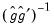 , where
, where 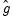 and
and 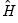 are the gradient (or score) and Hessian of the log likelihood evaluated at the ML estimates.
are the gradient (or score) and Hessian of the log likelihood evaluated at the ML estimates. 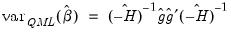
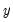 , but as with all QML estimation, caution is advised.
, but as with all QML estimation, caution is advised. belongs to the exponential family and that the conditional mean of
belongs to the exponential family and that the conditional mean of  is a (smooth) nonlinear transformation of the linear part
is a (smooth) nonlinear transformation of the linear part 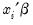 :
: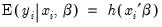
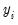 , it does not possess any efficiency properties. An alternative consistent estimate of the covariance is obtained if we impose the GLM condition that the (true) variance of
, it does not possess any efficiency properties. An alternative consistent estimate of the covariance is obtained if we impose the GLM condition that the (true) variance of  is proportional to the variance of the distribution used to specify the log likelihood:
is proportional to the variance of the distribution used to specify the log likelihood: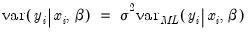
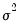 that is independent of
that is independent of 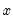 . The most empirically relevant case is
. The most empirically relevant case is 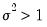 , which is known as
, which is known as 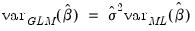
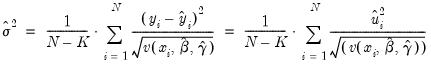
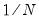 . When you select GLM standard errors, the estimated proportionality term
. When you select GLM standard errors, the estimated proportionality term 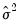 is reported as the variance factor estimate in EViews.
is reported as the variance factor estimate in EViews. 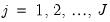 groups, and let
groups, and let 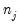 be the number of observations in group
be the number of observations in group 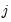 . Define the number of
. Define the number of 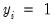 observations and the average of predicted values in group
observations and the average of predicted values in group 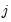 as:
as: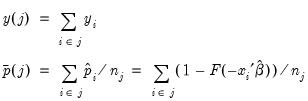
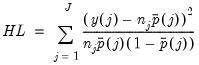
 distribution with
distribution with 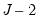 degrees of freedom. Note that these findings are based on a simulation where
degrees of freedom. Note that these findings are based on a simulation where 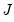 is close to
is close to 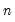 .
.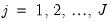 groups. Since
groups. Since  is binary, there are
is binary, there are 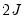 cells into which any observation can fall. Andrews (1988a, 1988b) compares the
cells into which any observation can fall. Andrews (1988a, 1988b) compares the 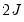 vector of the actual number of observations in each cell to those predicted from the model, forms a quadratic form, and shows that the quadratic form has an asymptotic
vector of the actual number of observations in each cell to those predicted from the model, forms a quadratic form, and shows that the quadratic form has an asymptotic  distribution if the model is specified correctly.
distribution if the model is specified correctly.  be an
be an 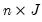 matrix with element
matrix with element 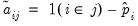 , where the indicator function
, where the indicator function 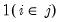 takes the value one if observation
takes the value one if observation  belongs to group
belongs to group  with
with 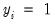 , and zero otherwise (we drop the columns for the groups with
, and zero otherwise (we drop the columns for the groups with 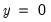 to avoid singularity). Let
to avoid singularity). Let 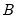 be the
be the 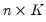 matrix of the contributions to the score
matrix of the contributions to the score 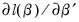 . The Andrews test statistic is
. The Andrews test statistic is  times the
times the 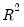 from regressing a constant (one) on each column of
from regressing a constant (one) on each column of 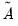 and
and 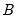 . Under the null hypothesis that the model is correctly specified,
. Under the null hypothesis that the model is correctly specified, 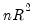 is asymptotically distributed
is asymptotically distributed 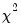 with
with 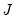 degrees of freedom.
degrees of freedom.