Save the scores from a principal components analysis of the series in a matrix.
Syntax
matrix_name.makepcomp(options) output_list
where the
output_list is a list of names identifying the saved components. EViews will save the first
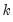
components corresponding to the
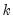
elements in
output_list, up to the total number of series in the group.
Options
scale=arg (default=“normload”) | Diagonal matrix scaling of the loadings and the scores: normalize loadings (“normload”), normalize scores (“normscores”), symmetric weighting (“symmetric”), user-specified (arg=number). |
cpnorm | Compute the normalization for the score so that cross-products match the target (by default, EViews chooses a normalization scale so that the moments of the scores match the target). |
eigval=vec_name | Specify name of vector to hold the saved the eigenvalues in workfile. |
eigvec=mat_name | Specify name of matrix to hold the save the eigenvectors in workfile. |
prompt | Force the dialog to appear from within a program. |
Covariance Options
cov=arg (default=“corr”) | Covariance calculation method: ordinary (Pearson product moment) covariance (“cov”), ordinary correlation (“corr”), Spearman rank covariance (“rcov”), Spearman rank correlation (“rcorr”), uncentered ordinary correlation (“ucorr”). Note that Kendall’s tau measures are not valid methods. |
wgt=name (optional) | Name of vector containing weights. The number of rows of the weight vector should match the number of rows in the original matrix. |
wgtmethod=arg (default = “sstdev” | Weighting method: frequency (“freq”), inverse of variances (“var”), inverse of standard deviation (“stdev”), scaled inverse of variances (“svar”), scaled inverse of standard deviations (“sstdev”). Only applicable for ordinary (Pearson) calculations where “weights=” is specified. Weights for rank correlation and Kendall’s tau calculations are always frequency weights. |
pairwise | Compute using pairwise deletion of observations with missing cases (pairwise samples). |
df | Compute covariances with a degree-of-freedom correction accounting for the mean (for centered specifications) and any partial conditioning variables. The default behavior in these cases is to perform no adjustment ( e.g. – compute sample covariance dividing by 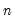 rather than 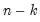 ). |
Examples
mat1.makepcomp comp1 comp2 comp3
saves the first three principal components (in normalized loadings form) to the workfile. The components will have variances that are proportional to the eigenvalues.
mat1.makepcomp(scale=normscore) comp1 comp2 comp3
normalizes the scores so that the resulting series have variances that are equal to 1.
You may change the scaling for the normalized components so that the cross-products equal 1, using the cpnorm option:
mat1.makepcomp(scale=normscore, cpnorm) comp1 comp2 comp3
Cross-references
See
“Saving Component Scores” for further discussion. See
Matrix::pcomp for tools to display the principal components results for the matrix.
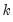 components corresponding to the
components corresponding to the 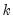 elements in output_list, up to the total number of series in the group.
elements in output_list, up to the total number of series in the group.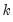 components corresponding to the
components corresponding to the 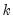 elements in output_list, up to the total number of series in the group.
elements in output_list, up to the total number of series in the group.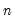 rather than
rather than 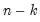 ).
).