Principal components analysis of the columns in a matrix.
Syntax
There are two forms of the pcomp command. The first form, which applies when displaying eigenvalue table output or graphs of the ordered eigenvalues, has only options and no command argument.
matrix_name.pcomp(options)
The second form, which applies to the graphs of component loadings, component scores, and biplots, uses the optional argument to determine which components to plot. In this form:
matrix_name.pcomp(options) [graph_list]
where the [graph_list] is an optional list of integers and/or vectors containing integers identifying the components to plot. Multiple pairs are handled using the method specified in the “mult=” option.
If the list of component indices omitted, EViews will plot only first and second components. Note that the order of elements in the list matters; reversing the order of two indices reverses the axis on which each component is displayed.
Options
out=arg (default=“table”) | Output: table of eigenvalue and eigenvector results (“table”), graphs of ordered eigenvalues (“graph”), graph of the eigenvectors (“loadings”), graph of the component scores (“scores”), biplot of the loadings and scores (“biplot”). Note: when specifying the eigenvalue graph (“out=graph”), the option keywords “scree” (scree graph), “diff” (difference in successive eigenvalues), and “cproport” (cumulative proportion of total variance) may be included to control the output. By default, EViews will display the scree graph. If you may one or more the three keywords, EViews will construct the graph using only the specified types. |
eigval=vec_name | Specify name of vector to hold the saved the eigenvalues in workfile. |
eigvec=mat_name | Specify name of matrix to hold the save the eigenvectors in workfile. |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Number of Component Options
fsmethod=arg (default=“simple”) | Component retention method: “bn” (Bai and Ng (2002)), “ah” (Ahn and Horenstein (2013)), “simple” (simple eigenvalue methods), “user” (user-specified value). Note the following: (1) If using simple methods, the minimum eigenvalue and cumulative proportions may be specified using “minigen=” and “cproport=”. (2) If setting “fsmethod=user” to provide a user-specified value, you must specify the value with “r=”. |
r=arg (default=1) | User-specified number of components to retain (for use when “fsmethod=user”). |
mineigen=arg (default=0) | Minimum eigenvalue to retain component (when “fsmethod=simple”). |
cproport=arg (default=1.0) | Cumulative proportion of eigenvalue total to attain (when “fsmethod=simple”). |
mfmethod=arg (default=“user”) | Maximum number of components used by selection methods: “schwert” (Schwert’s rule, default), “ah” (Ahn and Horenstein’s (2013) suggestion), “rootsize” ( 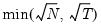 ), “size” ( 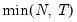 ) ), “user” (user specified value), where 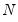 is the number of columns of the matrix and 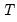 is the number of rows. (1) For use with all components retention methods apart from user-specified (“fsmethod=user”). (2) If setting “mfmethod=user”, you may specify the maximum number of components using “rmax=”. (3) Schwert’s rule sets the maximum number of components using the rule: let for 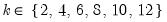 and let and let 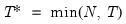 ; then the default maximum lag is given by ; then the default maximum lag is given by |
n=arg or rmax=arg (default=all) | User-specified maximum number of factors to retain (for use when “mfmethod=user”). |
fsic=arg (default=avg) | Component selection criterion when “fsmethod=bn”: “icp1” (ICP1), “icp2” (ICP2), “icp3” (ICP3), “pcp1” (PCP1), “pcp2” (PCP1), “pcp3” (ICP3), “avg” (average of all criteria ICP1 through PCP3). Component selection criterion when “fsmethod=ah”: “er” (eigenvalue ratio), “gr” (growth ratio), “avg” (average of eigenvalue ratio and growth ratio). Component selection when “fsmethod=simple”: “min” (minimum of: minimum eigenvalue, cumulative eigenvalue proportion, and maximum number of factors), “max” (maximum of: minimum eigenvalue, cumulative eigenvalue proportion, and maximum number of factors), “avg” (average the optimal number of factors as specified by the min and max rule, then round to the nearest integer). |
demeantime | Demeans observations across time prior to component selection procedures. |
sdizetime | Standardizes observations across time prior to component selection procedures. |
demeancross | Demeans observations across cross-sections prior to component selection procedures. |
sdizecross | Standardizes observations across cross-sections prior to component selection procedures. |
Covariance Options
cov=arg (default=“cov”) | Covariance calculation method: ordinary (Pearson product moment) covariance (“cov”), ordinary correlation (“corr”), Spearman rank covariance (“rcov”), Spearman rank correlation (“rcorr”), Kendall’s tau-b (“taub”), Kendall’s tau-a (“taua”), uncentered ordinary covariance (“ucov”), uncentered ordinary correlation (“ucorr”). |
wgt=name (optional) | Name of vector containing weights. The number of rows of the weight vector should match the number of rows in the original matrix. |
wgtmethod=arg (default = “sstdev” | Weighting method: frequency (“freq”), inverse of variances (“var”), inverse of standard deviation (“stdev”), scaled inverse of variances (“svar”), scaled inverse of standard deviations (“sstdev”). Only applicable for ordinary (Pearson) calculations where “weights=” is specified. Weights for rank correlation and Kendall’s tau calculations are always frequency weights. |
pairwise | Compute using pairwise deletion of observations with missing cases (pairwise samples). |
df | Compute covariances with a degree-of-freedom correction accounting for the mean (for centered specifications) and any partial conditioning variables. The default behavior in these cases is to perform no adjustment ( e.g. – compute sample covariance dividing by 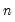 rather than 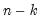 ). |
Graph Options
scale=arg, (default=“normload”) | Diagonal matrix scaling of the loadings and the scores: normalize loadings (“normload”), normalize scores (“normscores”), symmetric weighting (“symmetric”), user-specified (arg=number). |
mult =arg (default=“first”) | Multiple series handling: plot first against remainder (“first”), plot as x-y pairs (“pair”), lower-triangular plot (“lt”). |
nocenter | Do not center graphs around the origin. By default, EViews centers biplots around (0, 0). |
labels=arg, (default=“outlier”) | Observation labels for the scores: outliers only (“outlier”), all points (“all”), none (“none”). |
labelprob=number | Probability value for determining whether a point is an outlier according to the chi-square tests based on the squared Mahalanbois distance between the observation and the sample means (when using the “labels=outlier” option). |
autoscale=arg | Scale factor applied to the automatically specified loadings when displaying both loadings and scores). The default is to let EViews auto-choose a scale or to specify “userscale=” to scale the original loadings. |
userscale=arg | Scale factor applied to the original loadings when displaying both loadings and scores). The default is to let EViews auto-choose a scale, or to specify “autoscale=” to scale the automatically scaled loadings. |
cpnorm | Compute the normalization for the score so that cross-products match the target (by default, EViews chooses a normalization scale so that the moments of the scores match the target). |
Examples
freeze(tab1) mat1.pcomp(method=corr, eigval=v1, eigvec=m1)
stores the table view of the eigenvalues and eigenvectors of MAT1 in a table object named tab1, the eigenvalues in a vector named v1, and the eigenvectors in a matrix named m1.
mat1.pcomp(method=cov, out=graph)
displays the scree plot of the ordered eigenvalues computed from the covariance matrix.
mat1.pcomp(method=rcorr, out=biplot, scale=normscores)
displays a biplot where the scores are normalized to have variances that equal the eigenvalues of the Spearman correlation matrix computed for the series in MAT1.
Cross-references
See
“Principal Components” for further discussion. See also
“Covariance Analysis” for discussion of the preliminary computation.
Note that this view analyzes the eigenvalues and eigenvectors of a covariance (or other association) matrix computed from the series in a group or the columns of a matrix. You may use
Sym::eigen to examine the eigenvalues of a symmetric matrix.
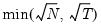 ), “size” (
), “size” (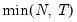 ), “user” (user specified value), where
), “user” (user specified value), where 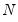 is the number of columns of the matrix and
is the number of columns of the matrix and 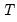 is the number of rows.
is the number of rows.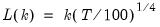
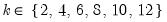 and let
and let 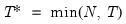 ; then the default maximum lag is given by
; then the default maximum lag is given by 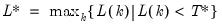
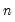 rather than
rather than 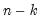 ).
).