Eigenvalues calculation for a symmetric matrix.
Syntax
There are two forms of the eigen command.
The first form, which applies when displaying eigenvalue table output or graphs of the ordered eigenvalues, has only options and no command argument.
sym_name.eigen(options)
The second form, which applies to the graphs of component loadings (specified with the option “out=loadings”) uses an optional argument to determine which components to plot. In this form:
sym_name.eigen(options) [graph_list]
where the graph_list is an optional list of integers and/or vectors containing integers identifying the components to plot. Multiple pairs are handled using the method specified in the “mult=” option.
If the list of component indices omitted, EViews will plot only first and second components. Note that the order of elements in the list matters; reversing the order of two indices reverses the axis on which each component is displayed.
Options
out=arg (default=“table”) | Output: table of eigenvalue and eigenvector results (“out=table”), graphs of ordered eigenvalues (“graph”), graph of the eigenvectors (“loadings”). Note: when specifying the eigenvalue graph (“out=graph”), the option keywords “scree” (scree graph), “diff” (difference in successive eigenvalues), and “cproport” (cumulative proportion of total variance) may be included to control the output. By default, EViews will display the scree graph. If you specify one or more of the keywords, EViews will construct the graph using only the specified types (i.e., if you specify “cproport”, a scree plot will not be provided unless requested). |
n=integer | Maximum number of components to retain when presenting table (“out=table”) or eigenvalue graph (“out=graph”) results. The default is to set 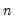 to the number of variables. EViews will retain the minimum number satisfying any of: “n=”, “mineig=” or “cproport=”. |
mineig=arg (default=0) | Minimum eigenvalue threshold value: we retain components with eigenvalues that are greater than or equal to the threshold. EViews will retain the minimum number satisfying any of: “n=”, “mineig=” or “cproport=”. |
cproport=arg (default = 1) | Cumulative proportion threshold value: we retain 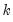 , the number of components required for the sum of the first 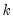 eigenvalues exceeds the specified value for the cumulative variance explained proportion. EViews will retain the minimum number satisfying any of: “n=”, “mineig=” or “cproport=”. |
eigval=vec_name | Specify name of vector to hold the saved the eigenvalues in workfile. |
eigvec=mat_name | Specify name of matrix to hold the save the eigenvectors in workfile. |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Graph Options
scale=arg, (default=“normload”) | Diagonal matrix scaling of the loadings: normalize loadings (“normload”), normalize scores (“normscores”), symmetric weighting (“symmetric”), user-specified power (arg=number). |
mult =arg (default=“first”) | Multiple series handling: plot first against remainder (“first”), plot as x-y pairs (“pair”), lower-triangular plot (“lt”). |
nocenter | Do not center graphs around the origin. |
Examples
sym s1 = @cov(g1)
freeze(tab1) s1.eigen(method=cor, eigval=v1, eigvec=m1)
The first line creates a group named g1 containing the four series x1, x2, x3, x4. The second line computes the correlation matrix S1 from the series in G1. The final line stores the table view of the eigenvalues and eigenvectors of S1 in a table object named tab1, the eigenvalues in a vector named v1, and the eigenvectors in a matrix named m1.
Cross-references
See
“Principal Components” for a discussion of principal components analysis on a group of series, which describes a superset of the tools for eigenvalue calculations offered by the sym matrix.
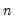 to the number of variables.
to the number of variables.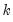 , the number of components required for the sum of the first
, the number of components required for the sum of the first 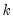 eigenvalues exceeds the specified value for the cumulative variance explained proportion.
eigenvalues exceeds the specified value for the cumulative variance explained proportion.