Transpose of a matrix object.
Syntax: @transpose(m)
m: matrix, vector, rowvector, sym
Return: matrix, rowvector, vector, sym
The result is a matrix object with the number of rows and columns and the element indices reversed from the original matrix. This function is an identity function for a sym, since a sym by definition is equal to its transpose.
Examples
matrix m1 = @mnrnd(5, 7)
matrix m1t = @transpose(m1)
creates a

matrix M1 filled with normal random variables, and the
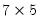
matrix transpose.
vector v1 = @mnrnd(10)
matrix m2 = v1 * @transpose(v1)
matrix m3 = @outer(v1, v1)
creates the
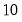
element vector V1 and forms the
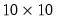
outer product matrices M2 and M3 both directly, and using the
@outer function.
Note that the transpose of matrix objects may also be obtained using the “@t” object data member function, as in
matrix m2a = v1 * v1.@t
Cross-references
 matrix M1 filled with normal random variables, and the
matrix M1 filled with normal random variables, and the 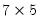 matrix transpose.
matrix transpose. matrix M1 filled with normal random variables, and the
matrix M1 filled with normal random variables, and the 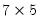 matrix transpose.
matrix transpose. matrix M1 filled with normal random variables, and the
matrix M1 filled with normal random variables, and the 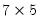 matrix transpose.
matrix transpose.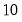 element vector V1 and forms the
element vector V1 and forms the 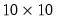 outer product matrices M2 and M3 both directly, and using the @outer function.
outer product matrices M2 and M3 both directly, and using the @outer function.