The VAR contains  variables
variables 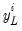 , observed at low frequency and
, observed at low frequency and 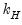 variables
variables 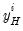 observed at the high frequency. Let
observed at the high frequency. Let
 variables
variables 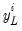 , observed at low frequency and
, observed at low frequency and 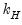 variables
variables 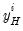 observed at the high frequency. Let
observed at the high frequency. Let  variables
variables 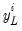 , observed at low frequency and
, observed at low frequency and 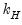 variables
variables 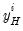 observed at the high frequency. Let
observed at the high frequency. Let 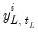 represent the i-th low frequency variable observed during low-frequency period
represent the i-th low frequency variable observed during low-frequency period 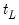
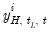 represent the i-th high frequency variable observed in the t-th high-frequency period during low-frequency period
represent the i-th high frequency variable observed in the t-th high-frequency period during low-frequency period 
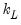 and
and  variables into the matrices
variables into the matrices 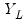 and
and 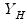 , respectively, and for brevity ignoring the intercepts and exogenous variables, we may write the VAR as:
, respectively, and for brevity ignoring the intercepts and exogenous variables, we may write the VAR as: | (49.1) |
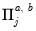 is
is  ,
,  is
is 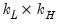 , and
, and 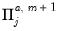 is
is  , for all
, for all 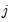 ,
, 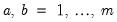 , and
, and 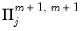 is
is 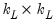 .
. , the stacked matrix of coefficients.
, the stacked matrix of coefficients.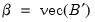 and the residual covariance matrix,
and the residual covariance matrix, 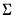 (
“Technical Background”).
(
“Technical Background”).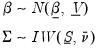 | (49.2) |
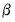 and
and 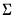 of:
of: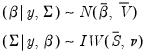 | (49.3) |
(49.4) |
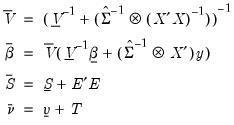 | (49.5) |
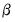 is constructed like the Litterman prior in standard Bayesian VARs.
is constructed like the Litterman prior in standard Bayesian VARs. 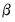 is assumed to be all zero, other than the own first lag terms. However the Ghysels prior differs slightly by allowing a different hyper-parameter for the own lag term depending on whether a variable is high or low frequency. Another crucial difference is that the variables are assumed to follow an AR(1) process in the high-frequency, so that when estimating in low-frequency space, the parameter is exponential.
is assumed to be all zero, other than the own first lag terms. However the Ghysels prior differs slightly by allowing a different hyper-parameter for the own lag term depending on whether a variable is high or low frequency. Another crucial difference is that the variables are assumed to follow an AR(1) process in the high-frequency, so that when estimating in low-frequency space, the parameter is exponential.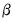 is similar to a Litterman prior, but with subtle differences to allow for the cross-frequency variances.
is similar to a Litterman prior, but with subtle differences to allow for the cross-frequency variances. Element | Mean | Variance | Dimension |
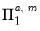 | 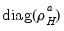 | 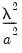 |  , ,  |
 | 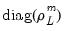 | 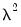 | 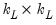 |
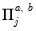 | 0 |  | 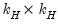 , ,  , , 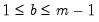 |
 | 0 | 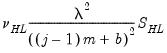 | 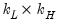 , , 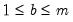 |
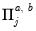 | 0 | 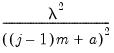 | 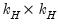 , , 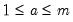 , ,  |
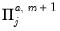 | 0 | 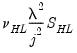 | 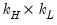 , , 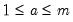 |
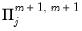 | 0 | 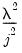 | 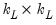 , , 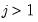 |
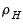 ,
, 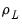 ,
, 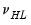 and
and 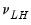 are hyper-parameters, and
are hyper-parameters, and 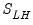 is a
is a 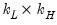 matrix with the (i,j)-th element equal to
matrix with the (i,j)-th element equal to 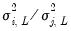 ,
,  ,
, 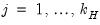 where the
where the 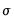 are taken from a univariate AR(1) estimation.
are taken from a univariate AR(1) estimation. .
.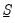 is formed by taking a scaled identity matrix or by scaling an initial estimate of the variance taken from a classical least squares U-MIDAS estimation:
is formed by taking a scaled identity matrix or by scaling an initial estimate of the variance taken from a classical least squares U-MIDAS estimation: | (49.6) |
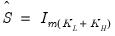 or
or 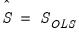 .
.