Background
We consider a standard multiple linear regression model with
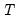
periods and
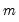
potential breaks (producing
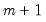
regimes). For the observations
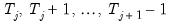
in regime

we have the regression model
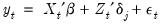 | (34.1) |
for the regimes
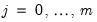
. Note that the regressors are divided into two groups. The
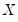
variables are those whose parameters do not vary across regimes, while the
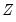
variables have coefficients that are regime-specific.
While it is slightly more convenient to define breakdates to be the last date of a regime, we follow EViews’s convention in defining the breakdate to be the first date of the subsequent regime. We tie down the endpoints by setting
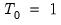
and
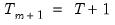
.
Once the number and identity of the breakpoints is determined, the model may be estimated using standard regression techniques. We may rewrite the equation specification as a standard regression equation
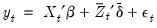 | (34.2) |
with fixed parameter vectors
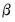
and

where

is an expanded set of regressors interacted with the set of dummy variables corresponding to each of the

regime segments.
The breakpoints may be known a priori or they be estimated using a variety of approaches. The breakpoint estimation methods that we consider may broadly be divided into two categories: global maximizers for the breakpoints and sequentially determined breakpoints.
Global Maximization
Bai and Perron (1998) describe global optimization procedures for identifying the
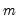
multiple breaks and associated coefficients which minimize the sums-of-squared residuals of the regression model
Equation (34.1).
If the desired number of breakpoints is known, the global
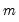
-break optimizers are the set of breakpoints and corresponding coefficient estimates that minimize the sum-of-squares for that model.
If the desired number of breakpoints is not known, we may specify a maximum number of breakpoints and employ testing to determine the “optimal” number of breakpoints. The various test approaches are outlined in detail in
“Global Maximizer Tests”, but briefly speaking, involve:
• Global tests of
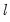
breaks versus none (Bai-Perron 1998). The test of
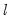
versus no breaks procedure may be applied sequentially beginning with a single break until the null is not rejected. Alternately, it may be applied to all breaks with the selected break being the highest statistically significant number of breaks, or it may employ the unweighted or weighted double maximum statistics (
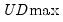
or
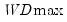
).
• Information criteria based model selection of the number of breaks (Yao 1988; Liu, Wi, and Zidek 1997), where we minimize the specified information criteria with respect to the number of breaks.
• Sequential tests of
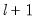
versus
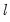
globally determined breakpoints. The procedure is applied sequentially, beginning with a single break, until the null is not rejected. This approach is a modified Bai (1997) method in which, at each test step, the
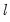
breakpoints under the null are obtained by global optimization, and the candidate breakpoints are obtained by sequential estimation.
Sequential Determination
Bai (1997) describes an intuitive approach for obtaining estimates for more than one break. The procedure involves sequential application of breakpoint tests.
• Begin with the full sample and perform a test of parameter constancy with unknown break. At each stage, test for breakpoints in breakpoint tests in each subsample. Add a breakpoint whenever a subsample null is rejected. (Alternately, one could test only the single subsample which shows the greatest improvement in the sum-of-squared residuals.) If any of the tests reject, add the specified breakpoint to the current set.
• Repeat the procedure until all of the subsamples do not reject the null hypothesis, or until the maximum number of breakpoints allowed or maximum subsample intervals to test is reached.
• Perform refinement so that breakpoints are re-estimated if they are obtained from a subsample containing more than one break. This procedure is required so that the breakpoint estimates have the same limiting distribution as those obtained from the global optimization procedure.
If the number of breakpoints is pre-specified, we simply estimate the specified number of breakpoints using the one-at-a-time method.
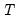 periods and
periods and 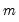 potential breaks (producing
potential breaks (producing 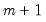 regimes). For the observations
regimes). For the observations 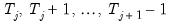 in regime
in regime  we have the regression model
we have the regression model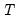 periods and
periods and 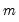 potential breaks (producing
potential breaks (producing 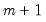 regimes). For the observations
regimes). For the observations 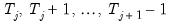 in regime
in regime  we have the regression model
we have the regression model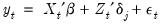
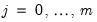 . Note that the regressors are divided into two groups. The
. Note that the regressors are divided into two groups. The 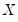 variables are those whose parameters do not vary across regimes, while the
variables are those whose parameters do not vary across regimes, while the 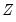 variables have coefficients that are regime-specific.
variables have coefficients that are regime-specific.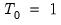 and
and 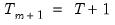 .
.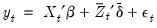
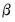 and
and  where
where  is an expanded set of regressors interacted with the set of dummy variables corresponding to each of the
is an expanded set of regressors interacted with the set of dummy variables corresponding to each of the  regime segments.
regime segments.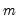 multiple breaks and associated coefficients which minimize the sums-of-squared residuals of the regression model
multiple breaks and associated coefficients which minimize the sums-of-squared residuals of the regression model
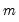 -break optimizers are the set of breakpoints and corresponding coefficient estimates that minimize the sum-of-squares for that model.
-break optimizers are the set of breakpoints and corresponding coefficient estimates that minimize the sum-of-squares for that model.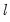 breaks versus none (Bai-Perron 1998). The test of
breaks versus none (Bai-Perron 1998). The test of 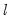 versus no breaks procedure may be applied sequentially beginning with a single break until the null is not rejected. Alternately, it may be applied to all breaks with the selected break being the highest statistically significant number of breaks, or it may employ the unweighted or weighted double maximum statistics (
versus no breaks procedure may be applied sequentially beginning with a single break until the null is not rejected. Alternately, it may be applied to all breaks with the selected break being the highest statistically significant number of breaks, or it may employ the unweighted or weighted double maximum statistics (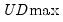 or
or 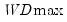 ).
).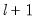 versus
versus 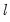 globally determined breakpoints. The procedure is applied sequentially, beginning with a single break, until the null is not rejected. This approach is a modified Bai (1997) method in which, at each test step, the
globally determined breakpoints. The procedure is applied sequentially, beginning with a single break, until the null is not rejected. This approach is a modified Bai (1997) method in which, at each test step, the 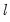 breakpoints under the null are obtained by global optimization, and the candidate breakpoints are obtained by sequential estimation.
breakpoints under the null are obtained by global optimization, and the candidate breakpoints are obtained by sequential estimation.