Background
Difference-in-difference estimation is a method of analyzing the impact of a treatment or policy on an outcome by comparing the difference in the outcome variable before and after treatment for those who participated in the treatment, with those who did not participate in the treatment.
Single Treatment Date
To begin, we shall suppose that there is a single treatment date,
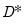
, on which some of the individuals in our study are given the treatment. The remainder of the individuals never receive treatment. We denote the treated individuals as belonging to group
T, and those not treated as belonging to group
NT. Along with data on whether an individual is treated, we also have time series data on an outcome variable,
Y, with periods both before and after the treatment date, for all individuals.
To estimate the average impact of the treatment on Y, we compare the difference in the mean of Y between the treated and never treated groups before and after the treatment date:
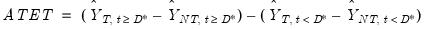 | (56.1) |
which we term the Average Treatment Effect for the Treated (ATET).
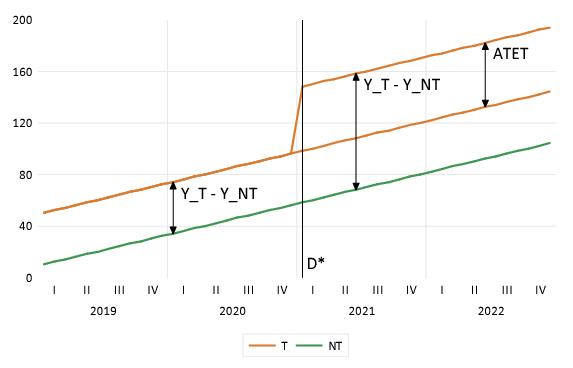
The ATET may be visualized as:
The calculation of the ATET may be embedded in an OLS regression structure, using the model
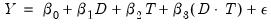 | (56.2) |
where
D is a dummy variable equal to 1 if the observation lies after

, and
T is a dummy variable equal to 1 if the observation is in the treated group. For notational simplicity, we ignore additional exogenous regressors in
Equation (56.2), though note that their inclusion does not change the behavior of the estimator.
It is easy to see that the ATET is equal to the value of
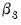
, which measures the marginal effect of being in the treatment group after
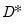
.
Alternately, the ATET may be estimated using a fixed effects model with fixed effects in both the group and time dimensions, and a dummy variable corresponding to whether the observations is treated (i.e., in the treated group and post-treatment date),
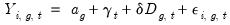 | (56.3) |
where
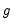
identifies the treatment (

) and the non-treatment (
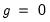
) groups, and
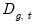
takes a value of 1 whenever a treatment group observation is actually treated. In this specification, the ATET is equal to the value of
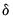
.
Further, the estimate
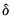
in
Equation (56.3) is numerically identical to the result obtained from the panel two-way fixed effects (TWFE) regression:
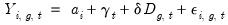 | (56.4) |
since the group identifier
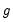
is constant for an individual
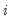
. In the latter specification, the group fixed effects have been replaced by individual cross-section effects.
Since the TWFE is estimated using ordinary least squares regression, all assumptions required for an OLS model are also required for DiD estimation by TWFE.
Crucially, for estimates of
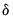
to be unbiased for the ATET, DiD requires an additional
parallel trends assumption. The parallel trends assumption requires that in the counter-factual where individuals in the treated group are not treated, the difference between the treatment group and the control group is constant through time. Intuitively, when comparing a treatment group to a never-treated or always-treated control group, unbiased estimation requires that the change in outcomes for the control group before and after the treatment date is a good measure of the (
unobserved) untreated change in the treatment group.
Multiple Treatment Dates
The model given by
Equation (56.1) assumes a single treatment date,
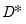
, with all individuals who will be treated, receiving treatment on the same date.
A natural extension to the single treatment model is to assume that different groups of individuals have different treatment dates:
Here we have 3 groups of individuals, some are never treated
NT, some are treated at the earlier date
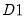
(
TE), and some are treated at a later date
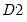
(
TL).
In such cases we are still interested in the average treatment effect for the treated (ATET), where the treatment effect is calculated as the effect on the trend post-treatment, whenever that treatment occurs.
The natural estimator for the ATET is this case is to simply extend the TWFE model
Equation (56.4) to incorporate more than 2 groups:
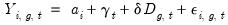 | (56.5) |
where

now indexes the multiple treatment date groups. Note that the presence of multiple treatment dates does not affect the form of the TWFE estimator.
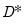 , on which some of the individuals in our study are given the treatment. The remainder of the individuals never receive treatment. We denote the treated individuals as belonging to group T, and those not treated as belonging to group NT. Along with data on whether an individual is treated, we also have time series data on an outcome variable, Y, with periods both before and after the treatment date, for all individuals.
, on which some of the individuals in our study are given the treatment. The remainder of the individuals never receive treatment. We denote the treated individuals as belonging to group T, and those not treated as belonging to group NT. Along with data on whether an individual is treated, we also have time series data on an outcome variable, Y, with periods both before and after the treatment date, for all individuals.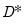 , on which some of the individuals in our study are given the treatment. The remainder of the individuals never receive treatment. We denote the treated individuals as belonging to group T, and those not treated as belonging to group NT. Along with data on whether an individual is treated, we also have time series data on an outcome variable, Y, with periods both before and after the treatment date, for all individuals.
, on which some of the individuals in our study are given the treatment. The remainder of the individuals never receive treatment. We denote the treated individuals as belonging to group T, and those not treated as belonging to group NT. Along with data on whether an individual is treated, we also have time series data on an outcome variable, Y, with periods both before and after the treatment date, for all individuals.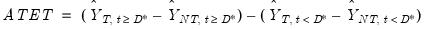
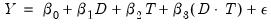
 , and
, and 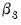 , which measures the marginal effect of being in the treatment group after
, which measures the marginal effect of being in the treatment group after 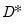 .
. 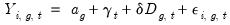
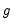 identifies the treatment (
identifies the treatment ( ) and the non-treatment (
) and the non-treatment (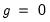 ) groups, and
) groups, and 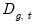 takes a value of 1 whenever a treatment group observation is actually treated. In this specification, the ATET is equal to the value of
takes a value of 1 whenever a treatment group observation is actually treated. In this specification, the ATET is equal to the value of 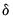 .
.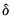 in
in
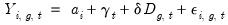
 is constant for an individual
is constant for an individual 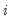 . In the latter specification, the group fixed effects have been replaced by individual cross-section effects.
. In the latter specification, the group fixed effects have been replaced by individual cross-section effects. to be unbiased for the ATET, DiD requires an additional
to be unbiased for the ATET, DiD requires an additional 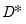 , with all individuals who will be treated, receiving treatment on the same date.
, with all individuals who will be treated, receiving treatment on the same date.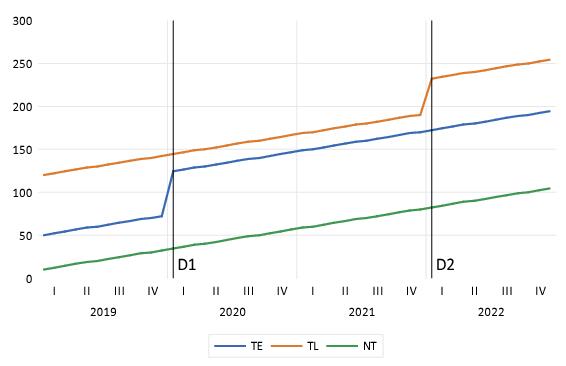
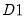
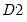 (
(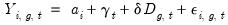
 now indexes the multiple treatment date groups. Note that the presence of multiple treatment dates does not affect the form of the TWFE estimator.
now indexes the multiple treatment date groups. Note that the presence of multiple treatment dates does not affect the form of the TWFE estimator.