References
Barrodale I. and F. D. K. Roberts (1974). “Solution of an Overdetermined System of Equations in the
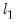
Norm,” Communications of the ACM, 17(6), 319-320.
Bassett, Gilbert Jr. and Roger Koenker (1982). “An Empirical Quantile Function for Linear Models with i.i.d. Errors,” Journal of the American Statistical Association, 77(378), 407-415.
Bofinger, E. (1975). “Estimation of a Density Function Using Order Statistics,” Australian Journal of Statistics, 17, 1-7.
Buchinsky, M. (1995). “Estimating the Asymptotic Covariance Matrix for Quantile Regression Models: A Monte Carlo Study,” Journal of Econometrics, 68, 303-338.
Chamberlain, Gary (1994). “Quantile Regression, Censoring and the Structure of Wages,” in Advances in Econometrics, Christopher Sims, ed., New York: Elsevier, 171-209.
Falk, Michael (1986). “On the Estimation of the Quantile Density Function,” Statistics & Probability Letters, 4, 69-73.
Hall, Peter and Simon J. Sheather, “On the Distribution of the Studentized Quantile,” Journal of the Royal Statistical Society, Series B, 50(3), 381-391.
He, Xuming and Feifang Hu (2002). “Markov Chain Marginal Bootstrap,” Journal of the American Statistical Association, 97(459), 783-795.
Hendricks, Wallace and Roger Koenker (1992). “Hierarchical Spline Models for Conditional Quantiles and the Demand for Electricity,” Journal of the American Statistical Association, 87(417), 58-68.
Jones, M. C. (1992). “Estimating Densities, Quantiles, Quantile Densities and Density Quantiles,” Annals of the Institute of Statistical Mathematics, 44(4), 721-727.
Kocherginsky, Masha, Xuming He, and Yunming Mu (2005). “Practical Confidence Intervals for Regression Quantiles,” Journal of Computational and Graphical Statistics, 14(1), 41-55.
Koenker, Roger (1994), “Confidence Intervals for Regression Quantiles,” in Asymptotic Statistics, P. Mandl and M. Huskova, eds., New York: Springer-Verlag, 349-359.
Koenker, Roger (2005). Quantile Regression. New York: Cambridge University Press.
Koenker, Roger and Gilbert Bassett, Jr. (1978). “Regression Quantiles,” Econometrica, 46(1), 33-50.
Koenker, Roger and Gilbert Bassett, Jr. (1982a). “Robust Tests for Heteroskedasticity Based on Regression Quantiles,” Econometrica, 50(1), 43-62.
Koenker, Roger and Gilbert Bassett, Jr. (1982b). “Tests of Linear Hypotheses and
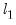
Estimation,”
Econometrica, 50(6), 1577-1584.
Koenker, Roger W. and Vasco D’Orey (1987). “Algorithm AS 229: Computing Regression Quantiles,” Applied Statistics, 36(3), 383-393.
Koenker, Roger and Kevin F. Hallock (2001). “Quantile Regression,” Journal of Economic Perspectives, 15(4), 143-156.
Koenker, Roger and Jose A. F. Machado (1999). “Goodness of Fit and Related Inference Processes for Quantile Regression,” Journal of the American Statistical Association, 94(448), 1296-1310.
Newey, Whitney K., and James L. Powell (1987). “Asymmetric Least Squares Estimation,” Econometrica, 55(4), 819-847.
Portnoy, Stephen and Roger Koenker (1997), “The Gaussian Hare and the Laplacian Tortoise: Computability of Squared-Error versus Absolute-Error Estimators,” Statistical Science, 12(4), 279-300.
Powell, J. (1984). “Least Absolute Deviations Estimation for the Censored Regression Model,” Journal of Econometrics, 25, 303-325.
Powell, J. (1986). “Censored Regression Quantiles,” Journal of Econometrics, 32, 143-155.
Powell, J. (1989). “Estimation of Monotonic Regression Models Under Quantile Restrictions,” in Non-parametric and Semiparametric Methods in Econometrics, W. Barnett, J. Powell, and G. Tauchen, eds., Cambridge: Cambridge University Press.
Siddiqui, M. M. (1960). “Distribution of Quantiles in Samples from a Bivariate Population,” Journal of Research of the National Bureau of Standards–B, 64(3), 145-150.
Silverman, B. W. (1986). Density Estimation for Statistics and Data Analysis, London: Chapman & Hall.
Welsh, A. H. (1988). “Asymptotically Efficient Estimation of the Sparsity Function at a Point,” Statistics & Probability Letters, 6, 427-432.
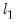 Norm,” Communications of the ACM, 17(6), 319-320.
Norm,” Communications of the ACM, 17(6), 319-320.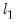 Norm,” Communications of the ACM, 17(6), 319-320.
Norm,” Communications of the ACM, 17(6), 319-320.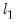 Norm,” Communications of the ACM, 17(6), 319-320.
Norm,” Communications of the ACM, 17(6), 319-320.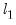 Estimation,” Econometrica, 50(6), 1577-1584.
Estimation,” Econometrica, 50(6), 1577-1584.