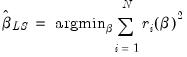
(33.1)
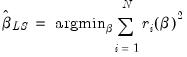 | (33.1) |
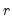 is given by
is given by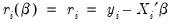 | (33.2) |
 enter the objective function on the right-hand side of
Equation (33.1) after squaring, the effects of outliers are magnified accordingly.
enter the objective function on the right-hand side of
Equation (33.1) after squaring, the effects of outliers are magnified accordingly. 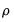 of the residuals:
of the residuals: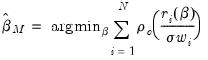 | (33.3) |
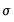 is a measure of the scale of the residuals,
is a measure of the scale of the residuals, 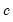 is an arbitrary positive tuning constant associated with the function, and where
is an arbitrary positive tuning constant associated with the function, and where 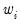 are individual weights that are generally set to 1, but may be set to:
are individual weights that are generally set to 1, but may be set to: | (33.4) |
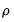 (Andrews, Bisquare, Cauchy, Fair, Huber-Bisquare, Logistic, Median, Talworth, Welsch) are outlined below along with the default values of the tuning constants:
(Andrews, Bisquare, Cauchy, Fair, Huber-Bisquare, Logistic, Median, Talworth, Welsch) are outlined below along with the default values of the tuning constants:Name |  | Default  |
Andrews | 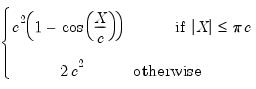 | 1.339 |
Bisquare | 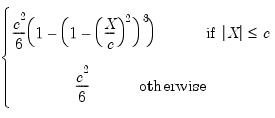 | 4.685 |
Cauchy | 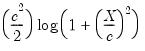 | 2.385 |
Fairl |  | 1.4 |
Huber | 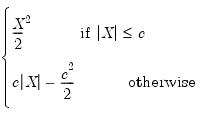 | 1.345 |
Logistic | 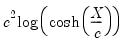 | 1.205 |
Median | 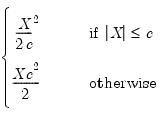 | 0.01 |
Talworth |  | 2.796 |
Welsch | 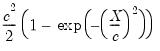 | 2.985 |
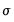 is known, then the
is known, then the 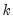 -vector of coefficient estimates
-vector of coefficient estimates 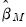 may be found using standard iterative techniques for solving the
may be found using standard iterative techniques for solving the  nonlinear first-order equations:
nonlinear first-order equations: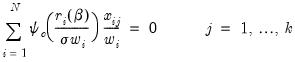 | (33.5) |
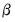 , where
, where 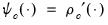 , the derivative of the
, the derivative of the 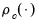 function, and
function, and 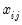 is the value of the j-th regressor for observation
is the value of the j-th regressor for observation 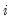 .
.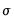 is not known, a sequential procedure is used that alternates between: (1) computing updated estimates of the scale
is not known, a sequential procedure is used that alternates between: (1) computing updated estimates of the scale 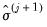 given coefficient estimates
given coefficient estimates 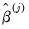 , and (2) using iterative methods to find the
, and (2) using iterative methods to find the 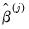 that solves
Equation (33.5) for a given
that solves
Equation (33.5) for a given 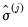 . The initial
. The initial 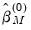 are obtained from ordinary least squares. The initial coefficients are used to compute a scale estimate,
are obtained from ordinary least squares. The initial coefficients are used to compute a scale estimate, 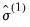 , and from that are formed new coefficient estimates
, and from that are formed new coefficient estimates  , followed by a new scale estimate
, followed by a new scale estimate  , and so on until convergence is reached.
, and so on until convergence is reached.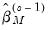 , the updated scale
, the updated scale 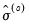 is estimated using one of three different methods: Mean Absolute Deviation – Zero Centered (MADZERO), Median Absolute Deviation – Median Centered (MADMED), or Huber Scaling:
is estimated using one of three different methods: Mean Absolute Deviation – Zero Centered (MADZERO), Median Absolute Deviation – Median Centered (MADMED), or Huber Scaling:MADZERO | 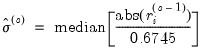 |
MADMED | 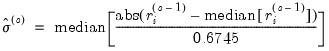 |
Huber | 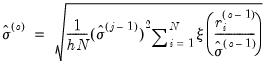 where 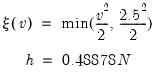 |
 are the residuals associated with
are the residuals associated with  and where the initial scale required for the Huber method is estimated by:
and where the initial scale required for the Huber method is estimated by: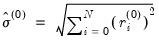 | (33.6) |
 statistic as
statistic as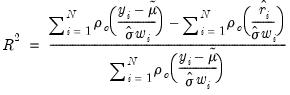
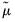 is the M-estimate from the constant-only specification.
is the M-estimate from the constant-only specification.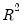 is calculated as:
is calculated as: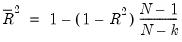 | (33.7) |
 statistic, and provide simulation results showing
statistic, and provide simulation results showing 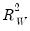 to be a better measure of fit than the robust
to be a better measure of fit than the robust 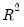 outlined above. The
outlined above. The 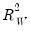 statistic is defined as
statistic is defined as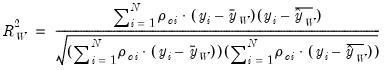 | (33.8) |
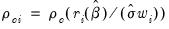 is the function of the residual value and
is the function of the residual value and  | (33.9) |
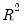 , an adjusted value of
, an adjusted value of 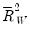 may be calculated from the unadjusted statistic
may be calculated from the unadjusted statistic | (33.10) |
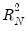 statistic is a robust version of a Wald test of the hypothesis that all of the coefficients are equal to zero. It is calculated using the standard Wald test quadratic form:
statistic is a robust version of a Wald test of the hypothesis that all of the coefficients are equal to zero. It is calculated using the standard Wald test quadratic form: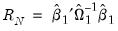 | (33.11) |
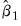 are the
are the 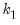 non-intercept robust coefficient estimates and
non-intercept robust coefficient estimates and 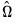 is the corresponding estimated covariance. Under the null hypothesis that all of the coefficients are equal to zero, the
is the corresponding estimated covariance. Under the null hypothesis that all of the coefficients are equal to zero, the 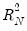 statistic is asymptotically distributed as a
statistic is asymptotically distributed as a 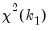 .
.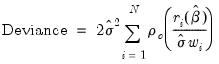 | (33.12) |
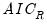 ), and a corresponding robust Schwarz Information Criterion (
), and a corresponding robust Schwarz Information Criterion (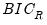 ):
):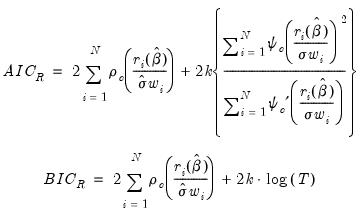 | (33.13) |
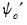 is the derivative of
is the derivative of 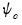 as outlined in Holland and Welsch (1977). See Ronchetti (1985) for details.
as outlined in Holland and Welsch (1977). See Ronchetti (1985) for details. that provide the smallest estimate of the scale
that provide the smallest estimate of the scale 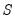 such that:
such that: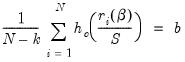 | (33.14) |
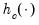 with tuning constant
with tuning constant 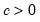 , where
, where 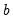 is taken to be
is taken to be 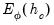 with
with  the standard normal. The breakdown value
the standard normal. The breakdown value 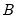 for this estimator is
for this estimator is 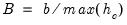 .
.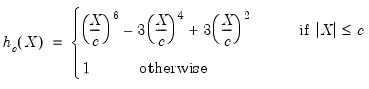 | (33.15) |
 using the Median Absolute Deviation, Zero Centered (MADZERO) method.
using the Median Absolute Deviation, Zero Centered (MADZERO) method. affects the objective function through
affects the objective function through 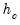 and
and 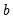 .
. 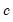 is typically chosen to achieve a desired breakdown value. EViews defaults to a
is typically chosen to achieve a desired breakdown value. EViews defaults to a 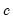 value of 1.5476 implying a breakdown value of 0.5. Other notable values for
value of 1.5476 implying a breakdown value of 0.5. Other notable values for 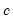 (with associated
(with associated 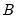 ) are:
) are: 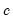 | 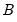 |
5.1824 | 0.10 |
4.0963 | 0.15 |
3.4207 | 0.20 |
2.9370 | 0.25 |
2.5608 | 0.30 |
1.9880 | 0.40 |
1.5476 | 0.50 |
 from the data and compute the least squares regression to obtain a
from the data and compute the least squares regression to obtain a  . By default
. By default 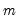 is set equal to
is set equal to 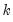 , the number of regressors. (Note that with the default
, the number of regressors. (Note that with the default 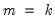 , the regression will produce an exact fit for the subsample.)
, the regression will produce an exact fit for the subsample.) refinements to the initial coefficient estimates using a variant of M-estimation which takes a single step toward the solution of
Equation (33.5) at every
refinements to the initial coefficient estimates using a variant of M-estimation which takes a single step toward the solution of
Equation (33.5) at every 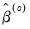 update. These modified M-estimate refinements employ the Bisquare function
update. These modified M-estimate refinements employ the Bisquare function 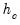 with tuning parameter and scale estimator
with tuning parameter and scale estimator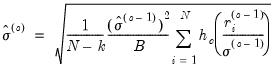 | (33.16) |
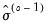 is the previous iteration's estimate of the scale and
is the previous iteration's estimate of the scale and 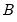 is the breakdown value defined earlier.
is the breakdown value defined earlier.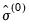 is obtained using MADZERO
is obtained using MADZERO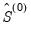 using MADZERO, and produce a final estimate of
using MADZERO, and produce a final estimate of 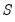 by iterating
Equation (33.16) (with
by iterating
Equation (33.16) (with 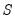 in place of
in place of  ) to convergence or until
) to convergence or until 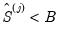 .
. 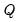 times. The best (smallest)
times. The best (smallest) 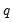 scale estimates are refined using M-estimation as in Step 2 with
scale estimates are refined using M-estimation as in Step 2 with  (or until convergence). The smallest scale from those refined scales is the final estimate of
(or until convergence). The smallest scale from those refined scales is the final estimate of 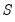 , and the final coefficient estimates are the corresponding estimates of
, and the final coefficient estimates are the corresponding estimates of  .
.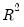 for S-estimation is given by:
for S-estimation is given by: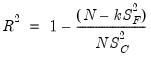 | (33.17) |
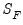 is the estimate of the scale from the final estimation, and
is the estimate of the scale from the final estimation, and  is an estimate of the scale from S-estimation with only a constant as a regressor.
is an estimate of the scale from S-estimation with only a constant as a regressor.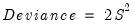 | (33.18) |
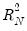 statistic is identical to the one computed for M-estimation. See
“Rn-squared Statistic” for discussion.
statistic is identical to the one computed for M-estimation. See
“Rn-squared Statistic” for discussion.Type I (default) | 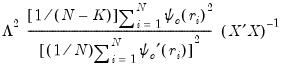 |
Type II | 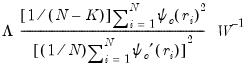 |
Type III | 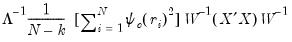 |
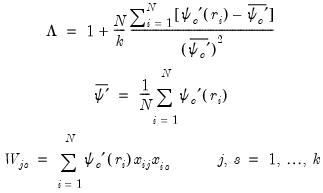 | (33.19) |
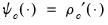 and
and 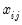 is the value of the j-th regressor for observation
is the value of the j-th regressor for observation 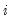 .
.