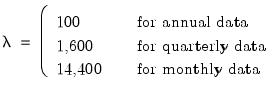Hodrick-Prescott Filter
The Hodrick-Prescott Filter is a widely employed smoothing method for obtaining a smooth estimate of the long-term trend component of a series. The method was first proposed in a working paper (circulated in the early 1980’s and published in 1997) by Hodrick and Prescott to analyze postwar U.S. business cycles.
EViews 14 enhances the existing routines with support for the iterated (boosted) HP filter proposed by Phillips and Shi (2020).
Technically, the Hodrick-Prescott (HP) filter is a two-sided linear filter that computes the smoothed series
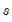
of
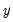
by minimizing the variance of
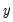
around
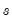
, subject to a penalty that constrains the second difference of
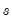
. The HP filter chooses the values of
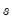
to minimize:
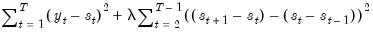 | (11.105) |
The
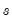
series is often referred to as the trend series. The cyclical component
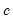
of the original series can be computed as
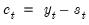
.
The penalty parameter
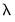
controls the smoothness of
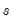
. The larger the
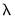
, the smoother the
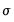
. As
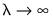
,
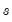
approaches a linear trend.
Phillips and Shi (2020) have proposed iterating the HP filter to produce a “smarter smoothing device.” This
boosted HP filter takes the cyclical series,
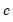
and runs the filter on it one more time to produce a new smoothed and cycle series. The filtering process is repeated, producing a further smoothed series at each iteration. The advantage of this iterative procedure is that the final smoothed series is less reliant on the choice of
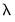
. Phillips and Shi recommend repeating the process either after a set number of iterations, or through the use of information criteria to decide the optimal number of iterations.
To smooth the series using the Hodrick-Prescott filter, choose :
First, provide a name for the . EViews will suggest a name, but you can always enter a name of your choosing. If you wish to save a , specify a name in the edit field.
Next, specify an integer value for the smoothing parameter,
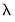
. You may specify
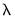
directly by clicking on the radio button and entering a value in the edit field, or you may specify a value using the frequency power rule of Ravn and Uhlig (2002) (the number of periods per year divided by 4, raised to a power, and multiplied by 1600 by clicking on the and entering a value in the edit field.
By default, EViews will fill the defaults using the Ravn and Uhlig method with a power rule of 2, yielding the original Hodrick and Prescott values for
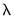
:
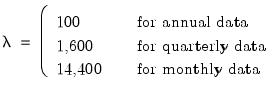 | (11.106) |
Ravn and Uhlig recommend using a power value of 4. EViews will round any non-integer values that you enter.
The Boosting section of the dialog offers settings for iterative boosting of the HP filter. You may choose between stopping based on the maximum number of iterations or using an Information criteria.
If you click on , EViews will stop based on the entry in the Max. Iterations edit field. By default, there will be no boosting as only one iteration of the filter will be performed.
Selecting the Information criteria radio button instructs EViews to select the optimal number of iterations using information criteria. The Max. Iterations edit field should be used to specify the number of iterations to be considered.
When you click on OK, EViews displays a graph of the filtered series together with the original series. Note that only data in the current workfile sample are filtered. Observations for the smoothed and cyclical series outside the current sample will be filled with NAs.
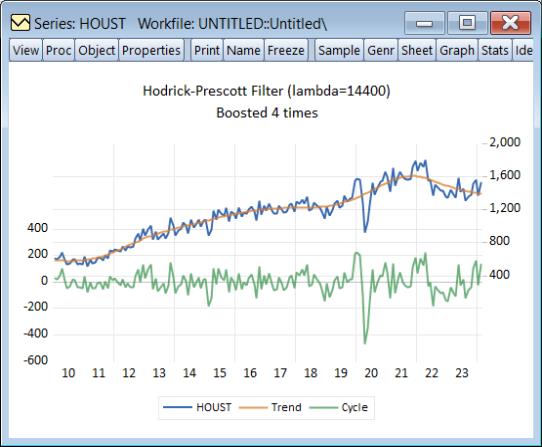
For example, we may download housing starts data from the Federal Reserve of St. Louis database:
dbopen(type=fred, server=api.stlouisfed.org/fred)
wfcreate m 1959M01 2024M02
fetch(d=fred) houst
smpl 2010 2024m02
and then perform HP filtering with 5 iterations on the HOUST series using values from 2010m01 through 2024m02:
The newly created HPTREND series contains the smoothed values of HOUST.
Note that only data in the current workfile sample are filtered. Data for the smoothed series outside the current sample are filled with NAs.
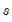 of
of 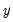 by minimizing the variance of
by minimizing the variance of 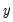 around
around 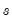 , subject to a penalty that constrains the second difference of
, subject to a penalty that constrains the second difference of 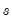 . The HP filter chooses the values of
. The HP filter chooses the values of 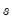 to minimize:
to minimize: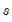 of
of 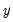 by minimizing the variance of
by minimizing the variance of 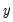 around
around 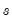 , subject to a penalty that constrains the second difference of
, subject to a penalty that constrains the second difference of 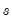 . The HP filter chooses the values of
. The HP filter chooses the values of 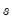 to minimize:
to minimize: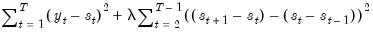
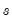 series is often referred to as the trend series. The cyclical component
series is often referred to as the trend series. The cyclical component 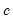 of the original series can be computed as
of the original series can be computed as 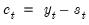 .
.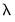 controls the smoothness of
controls the smoothness of 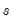 . The larger the
. The larger the 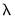 , the smoother the
, the smoother the 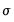 . As
. As 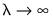 ,
, 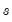 approaches a linear trend.
approaches a linear trend.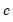 and runs the filter on it one more time to produce a new smoothed and cycle series. The filtering process is repeated, producing a further smoothed series at each iteration. The advantage of this iterative procedure is that the final smoothed series is less reliant on the choice of
and runs the filter on it one more time to produce a new smoothed and cycle series. The filtering process is repeated, producing a further smoothed series at each iteration. The advantage of this iterative procedure is that the final smoothed series is less reliant on the choice of 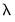 . Phillips and Shi recommend repeating the process either after a set number of iterations, or through the use of information criteria to decide the optimal number of iterations.
. Phillips and Shi recommend repeating the process either after a set number of iterations, or through the use of information criteria to decide the optimal number of iterations.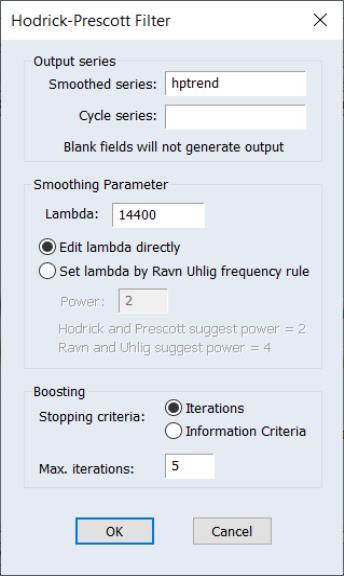
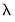 . You may specify
. You may specify 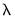 directly by clicking on the
directly by clicking on the 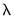 :
: