Testing for Bubbles
Identification of bubbles in financial asset prices is an important topic in financial econometrics that has received considerable attention over the past decade (see Gürkaynak (2008) and Homm and Breitung (2012) for literature surveys).
EViews includes tests for detection of bubbles based on the ADF unit root tests (see
“The Augmented Dickey-Fuller (ADF) Test”). These testing strategies were developed in Phillips et al. (2011, PWY) and Phillips et al. (2015, PSY).
The tests are based on a model of asset prices of:
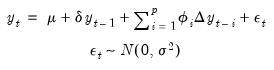 | (11.108) |
Where

is the price of the asset,
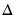
is the difference operator, and
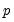
is a given number of lags.
A test for the presence of a bubble in the asset price is equivalent to testing for an explosion in the price, i.e. a null hypothesis of
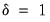
versus an alternative hypothesis of
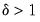
in the above equation, which is a one-sided version of the standard ADF test.
Since bubbles are a local phenomenon (i.e. an explosive root in the price of the asset is temporary), tests for
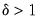
should use data over a short period, rather than the entire sample.
With that in mind, the first test performed by EViews produces a series of rolling ADF (RADF) tests. In this rolling framework, an initial ADF test is calculated over a short window of observations at the start of the data sample and the test statistic recorded. Then increment the observations by one (both start date and end date are incremented) and perform and record the ADF test again. Continue until the end of the data sample is reached. The maximum of the series of ADF statistics is then the RADF test-statistic.
PWY suggest an alternative approach which is to expand the window, rather than roll it. That is, after estimating the initial small window, only increment the end date of the sample at each iteration, rather than both the start and end date. They term the maximum of these expanding statistics the SADF (supremum ADF) test statistic.
PSY extend the approach further by proposing a rolling and expanding window. They begin by estimating the SADF statistic for a given small starting window. Once the SADF statistic has been computed over the expanding samples, a second set of SADF statistics is calculated, but by incrementing the start date of the initial window by one period. The maximum of the resulting series of maximums is called the generalized supremum ADF (GSADF) statistic.
The asymptotic distribution of all three test statistics is unknown, and critical values are produced by bootstrap. Under the Null hypothesis, the ADF equation can be written as:
 | (11.109) |
This equation is estimated by least squares, and an estimate of the residuals,
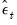
, are computed. These
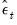
are demeaned and then resampled into a random order.
With the resampled

, estimates of

are generated using the left hand side of equation (2), with initial values of
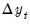
taken from the original data. From these newly generated
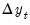
the RADF, SADF or GSADF test statistic is computed. This procedure is repeated many times to produce a distribution of test statistics from which critical value or p-values can be produced.
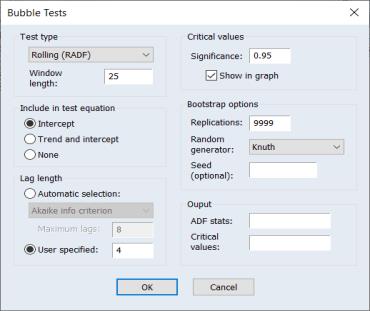
To perform a bubble test in EViews, open the series and click on View/Time Series Diagnostics/Bubble Tests…
The Test type dropdown field allows you to select which type of test you would like to run: Rolling ADF (RADF), expanding window supremum ADF (SADF), or global supremum ADF (GSADF). If RADF is selected, the Window length: field is used to specify the number of observations in each iteration of the rolling tests. If SADF or GSADF is selected, the Initial window length: field is used to specify the number of observations in the first iteration of the expanding tests.
You can specify to include a constant (Intercept), both a constant and a trend term (Trend and intercept), or neither (None) in the ADF test equation using the Include in test equation box.
The Lag length box is used to select either the number of lags to use (User specified:), or the information criteria used, and the maximum number of lags to compare, for Automatic selection:.
The Bootstrap options box defines the options used for the bootstrap procedure used to produce the test p-values. Use the Draws: box to enter the number of bootstrap iterations, and the RNG type: and Seed fields are used to specify the type of random number generator and its seed value.
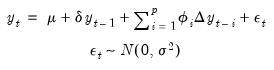
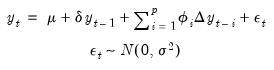
 is the price of the asset,
is the price of the asset, 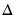 is the difference operator, and
is the difference operator, and 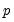 is a given number of lags.
is a given number of lags.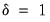 versus an alternative hypothesis of
versus an alternative hypothesis of 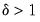 in the above equation, which is a one-sided version of the standard ADF test.
in the above equation, which is a one-sided version of the standard ADF test.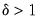 should use data over a short period, rather than the entire sample.
should use data over a short period, rather than the entire sample.
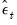 , are computed. These
, are computed. These 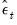 are demeaned and then resampled into a random order.
are demeaned and then resampled into a random order. , estimates of
, estimates of  are generated using the left hand side of equation (2), with initial values of
are generated using the left hand side of equation (2), with initial values of 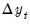 taken from the original data. From these newly generated
taken from the original data. From these newly generated 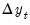 the RADF, SADF or GSADF test statistic is computed. This procedure is repeated many times to produce a distribution of test statistics from which critical value or p-values can be produced.
the RADF, SADF or GSADF test statistic is computed. This procedure is repeated many times to produce a distribution of test statistics from which critical value or p-values can be produced.