Background
We begin with a standard multiple linear regression model with

observations and
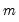
potential thresholds (producing
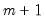
regimes). (While we will use
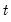
to index the
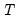
observations, there is nothing in the structure of the model that requires time series data.)
For the observations in regime

we have the linear regression specification
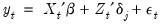 | (35.1) |
Note that the regressors are divided into two groups. The

variables are those whose parameters do not vary across regimes, while the
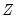
variables have coefficients that are regime-specific.
Suppose that there is an observable
threshold variable 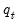
and strictly increasing
threshold values 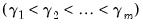
such that we are in regime
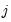
if and only if:
where we set
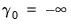
and

. Thus, we are in regime
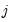
if the value of the threshold variable is at least as large as the
j-th threshold value, but not as large as the
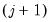
-th threshold. (Note that we follow EViews convention by defining the threshold values as the first values of each regime.)
For example, in the single threshold, two regime model, we have:
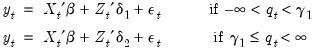 | (35.2) |
Using an indicator function
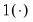
which takes the value 1 if the expression is true and 0 otherwise and defining
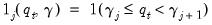
, we may combine the
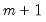
individual regime specifications into a single equation:
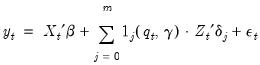 | (35.3) |
The identity of the threshold variable
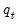
and the regressors
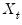
and
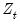
will determine the type of TR specification. If
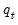
is the
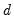
-th lagged value of
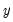
,
Equation (35.3) is a self-exciting (SE) model with
delay 
; if it’s not a lagged dependent, it's a conventional TR model. If the regressors
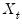
and
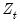
contain only a constant and lags of the dependent variable, we have an autoregressive (AR) model. Thus, a SETAR model is a threshold regression that combines an autoregressive specification with a lagged dependent threshold variable.
Given the threshold variable and the regression specification in
Equation (35.1), we wish to find the coefficients
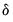
and
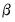
, and usually, the threshold values
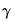
. We may also use model selection to identify the threshold variable
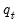
.
Nonlinear least squares is an natural approach for estimating the parameters of the model. If we define the sum-of-squares objective function
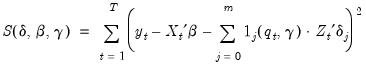 | (35.4) |
and we may obtain threshold regression estimates by minimizing

with respect to the parameters.
Taking advantage of the fact that for a given
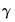
, say
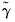
, minimization of the concentrated objective
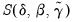
is a simple least squares problem, we can view estimation as finding the set of thresholds and corresponding OLS coefficient estimates that minimize the sum-of-squares across
all possible sets of
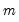
-threshold partitions.
This basic estimation setup is well known from the breakpoint testing and regression literature (see, for example, Hansen, 2001 and Perron, 2006), and indeed, by permuting the observation index so that the threshold variable is non-decreasing, one sees that estimation of the threshold and breakpoint models are fundamentally equivalent (Bai and Perron, 2003), In essence, threshold regressions can be thought of as breakpoint least squares regressions with data reordered with respect to the threshold variable. Alternately, breakpoint regressions may be thought of as threshold regressions with time as the threshold variable.
Accordingly, the discussion of breakpoint testing (
“Multiple Breakpoint Tests”) and estimation (
“Least Squares with Breakpoints”) may generally be applied in the current context. We will assume for our purposes that you are familiar with, or can refer to this material, and in the interest of brevity, we will minimize the amount of repetition in our discussion below.
 observations and
observations and 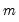 potential thresholds (producing
potential thresholds (producing 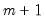 regimes). (While we will use
regimes). (While we will use 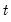 to index the
to index the 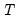 observations, there is nothing in the structure of the model that requires time series data.)
observations, there is nothing in the structure of the model that requires time series data.) observations and
observations and 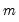 potential thresholds (producing
potential thresholds (producing 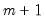 regimes). (While we will use
regimes). (While we will use 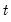 to index the
to index the 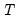 observations, there is nothing in the structure of the model that requires time series data.)
observations, there is nothing in the structure of the model that requires time series data.) we have the linear regression specification
we have the linear regression specification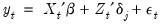
 variables are those whose parameters do not vary across regimes, while the
variables are those whose parameters do not vary across regimes, while the 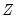 variables have coefficients that are regime-specific.
variables have coefficients that are regime-specific.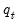 and strictly increasing
and strictly increasing 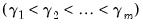 such that we are in regime
such that we are in regime 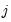 if and only if:
if and only if: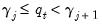
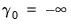 and
and  . Thus, we are in regime
. Thus, we are in regime 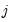 if the value of the threshold variable is at least as large as the
if the value of the threshold variable is at least as large as the 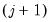 -th threshold. (Note that we follow EViews convention by defining the threshold values as the first values of each regime.)
-th threshold. (Note that we follow EViews convention by defining the threshold values as the first values of each regime.)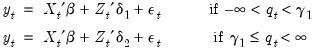
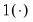 which takes the value 1 if the expression is true and 0 otherwise and defining
which takes the value 1 if the expression is true and 0 otherwise and defining 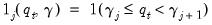 , we may combine the
, we may combine the 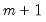 individual regime specifications into a single equation:
individual regime specifications into a single equation: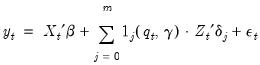
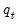 and the regressors
and the regressors 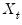 and
and 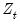 will determine the type of TR specification. If
will determine the type of TR specification. If 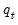 is the
is the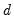 -th lagged value of
-th lagged value of 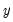 ,
,
 ; if it’s not a lagged dependent, it's a conventional TR model. If the regressors
; if it’s not a lagged dependent, it's a conventional TR model. If the regressors 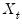 and
and 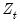 contain only a constant and lags of the dependent variable, we have an autoregressive (AR) model. Thus, a SETAR model is a threshold regression that combines an autoregressive specification with a lagged dependent threshold variable.
contain only a constant and lags of the dependent variable, we have an autoregressive (AR) model. Thus, a SETAR model is a threshold regression that combines an autoregressive specification with a lagged dependent threshold variable. 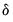 and
and 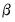 , and usually, the threshold values
, and usually, the threshold values 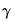 . We may also use model selection to identify the threshold variable
. We may also use model selection to identify the threshold variable 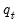 .
.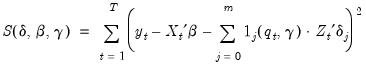
 with respect to the parameters.
with respect to the parameters. 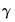 , say
, say 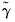 , minimization of the concentrated objective
, minimization of the concentrated objective 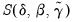 is a simple least squares problem, we can view estimation as finding the set of thresholds and corresponding OLS coefficient estimates that minimize the sum-of-squares across
is a simple least squares problem, we can view estimation as finding the set of thresholds and corresponding OLS coefficient estimates that minimize the sum-of-squares across 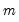 -threshold partitions.
-threshold partitions.