LU decomposition of matrix.
Syntax: @lu(M, L, U)
M: matrix
L: matrix
U: matrix
Return: matrix (P)
Performs an LU decomposition with partial (row) pivoting of the matrix M:
• if
M is a square
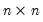
produce a unit lower triangular matrix,
L, an upper triangular matrix,
U, and a row permutation matrix,
P, such that
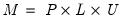
.
• if
M is a non-square
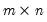
matrix, if
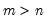
,
L will be unit lower trapezoidal (rather than triangular), and if
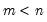
,
U will be upper trapezoidal (rather than triangular).
Examples
matrix m = @mnrnd(10, 8)
matrix lmat
matrix umat
matrix pmat = @lu(m, lmat, umat)
generates the random matrix M, then performs the LU decomposition returning PMAT and yielding updated LMAT, UMAT.
The following commands validate the definition
matrix m1 = pmat * lmat * umat
matrix diff = m - m1
since DIFF equals zero.
Cross-references
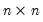 produce a unit lower triangular matrix, L, an upper triangular matrix, U, and a row permutation matrix, P, such that
produce a unit lower triangular matrix, L, an upper triangular matrix, U, and a row permutation matrix, P, such that 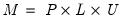 .
.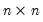 produce a unit lower triangular matrix, L, an upper triangular matrix, U, and a row permutation matrix, P, such that
produce a unit lower triangular matrix, L, an upper triangular matrix, U, and a row permutation matrix, P, such that 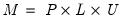 .
.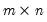 matrix, if
matrix, if 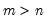 ,
, 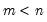 ,
,