Singular value decomposition (full) of matrix
Syntax: @svdfull(m1, m2, m3)
m1: matrix, sym
m2: matrix
m3: matrix, sym
Return: matrix
Performs a singular value decomposition of the matrix m1.
The matrix
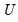
is returned by the function, the matrix
m2 will be assigned (resized if necessary) the matrix
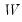
, and the matrix
m3 will be assigned (resized if necessary) the other matrix,
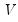
, of the decomposition. The singular value decomposition satisfies:
where
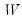
is a diagonal matrix with the singular values along the diagonal. Singular values close to zero indicate that the matrix may not be of full rank. See the
@rank function for a related discussion.
Examples
matrix x = @mnrnd(5, 7)
matrix w
matrix v
matrix u = @svdfull(x, w, v)
performs the full SVD of the matrix X. U is
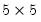
, W is
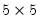
diagonal matrix with singular values on the diagonal, and V is
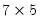
.
Alternately, if the rank is less than the number of rows,
matrix x = @mnrnd(7, 5)
matrix u = @svdfull(x, w, v)
then U is
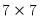
, W is a
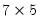
matrix with the singular values on the main diagonal and V is a
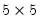
matrix.
In both cases, the following demonstrate the properties of the decomposition:
sym i1 = @inner(u)
sym i2 = @inner(v)
matrix x1 = u * w * v.@t
where I1 and I2 and the identity matrix, and X1 is equal to X.
Cross-references
See also
@svd,
@cholesky,
@lu, and
@qr.
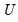 is returned by the function, the matrix m2 will be assigned (resized if necessary) the matrix
is returned by the function, the matrix m2 will be assigned (resized if necessary) the matrix 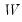 , and the matrix m3 will be assigned (resized if necessary) the other matrix,
, and the matrix m3 will be assigned (resized if necessary) the other matrix, 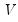 , of the decomposition. The singular value decomposition satisfies:
, of the decomposition. The singular value decomposition satisfies: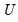 is returned by the function, the matrix m2 will be assigned (resized if necessary) the matrix
is returned by the function, the matrix m2 will be assigned (resized if necessary) the matrix 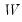 , and the matrix m3 will be assigned (resized if necessary) the other matrix,
, and the matrix m3 will be assigned (resized if necessary) the other matrix, 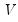 , of the decomposition. The singular value decomposition satisfies:
, of the decomposition. The singular value decomposition satisfies: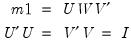
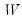 is a diagonal matrix with the singular values along the diagonal. Singular values close to zero indicate that the matrix may not be of full rank. See the
is a diagonal matrix with the singular values along the diagonal. Singular values close to zero indicate that the matrix may not be of full rank. See the
 , W is
, W is  diagonal matrix with singular values on the diagonal, and V is
diagonal matrix with singular values on the diagonal, and V is 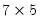 .
.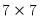 , W is a
, W is a 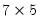 matrix with the singular values on the main diagonal and V is a
matrix with the singular values on the main diagonal and V is a 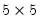 matrix.
matrix.