Compute dependent (second generation) panel unit root tests on a group of series.
Syntax
group_name.uroot2(options)
where group_name is the name of a group object.
Options
General Options
type=arg (default=“panic”) | Type of unit root test: PANIC - Bai and Ng (2004) (“panic”), CIPS - Pesaran (2007) (“cips”). Note: (1) when performing PANIC testing, factor selection, MQ, ADF lag selection, VAR lag selection (possibly), long-run variance (possibly), and p-value simulation options are relevant. (2) when perform CIPS testing, ADF lag selection options are relevant. |
exog=arg (default=“constant”) | Exogenous deterministic variables to include for each cross-section: “none” (no deterministic variables), “constant” (only a constant), “trend” (both a constant and trend). |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
ADF Lag Selection Options
adflagmethod=arg (default=“sic”) | Method for selecting lag length (number of first difference terms) to be included in the Dickey-Fuller test regression or number of lags in the AR spectral density estimator: “aic” (Akaike), “sic” (Schwarz), “hqc” (Hannan-Quinn), “msaic” (Modified Akaike), “msic” (Modified Schwarz), “mhqc” (Modified Hannan-Quinn), “tstat” (Ng-Perron first backward significant t-statistic). |
adflag=integer | Use-specified fixed lag. |
adfmaxlag=integer | Maximum lag length to consider when performing automatic lag length selection. Note: default is Schwert’s rule: let for 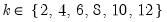 and let and let 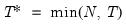 ; then the default maximum lag is given by ; then the default maximum lag is given by |
adflagpval=arg (default=0.1) | Probability value for use in the t-statistic automatic lag selection method (“lagmethod = tstat”). |
PANIC Number of Factor Selection Options
fsmethod=arg (default=“bn”) | Factor retention selection method: “bn” (Bai and Ng (2002)), “ah” (Ahn and Horenstein (2013)), “simple” (simple eigenvalue methods), “user” (user-specified value). Note the following: (1) If using simple methods, the minimum eigenvalue and cumulative proportions may be specified using “minigen=” and “cproport=”. (2) If setting “fsmethod=user” to provide a user-specified value, you must specify the value with “r=”. |
r=arg (default=1) | User-specified number of factors to retain (for use when “fsmethod=user”). |
mineigen=arg (default=0) | Minimum eigenvalue to retain factor (when “fsmethod=simple”). |
cproport=arg (default=1.0) | Cumulative proportion of eigenvalue total to attain (when “fsmethod=simple”). |
mfmethod=arg | Maximum number of factors used by selection methods: “schwert” (Schwert’s rule, default), “ah” (Ahn and Horenstein’s (2013) suggestion), “rootsize” ( 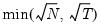 ), “size” ( 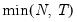 ) ), “user” (user specified value). (1) For use with all factor retention methods apart from user-specified (“fsmethod=user”). (2) If setting “mfmethod=user”, you may specify the maximum number of factors using “rmax=”. (3) Schwert’s rule sets the maximum number of factors using the rule: let for 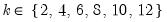 and let and let 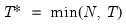 ; then the default maximum lag is given by ; then the default maximum lag is given by |
rmax=arg (default=all) | User-specified maximum number of factors to retain (for use when “mfmethod=user”). |
fsic=arg (default=avg) | Factor selection criterion (when “fsmethod=bn”): “icp1” (ICP1), “icp2” (ICP2), “icp3” (ICP3), “pcp1” (PCP1), “pcp2” (PCP1), “pcp3” (ICP3), “avg” (average of all criteria ICP1 through PCP3). Factor selection criterion (when “fsmethod=ah”): “er” (eigenvalue ratio), “gr” (growth ratio), “avg” (average of eigenvalue ratio and growth ratio). Factor selection criterion (when “fsmethod=simple”): “min” (minimum of: minimum eigenvalue, cumulative eigenvalue proportion, and maximum number of factors), “max” (maximum of: minimum eigenvalue, cumulative eigenvalue proportion, and maximum number of factors), “avg” (average the optimal number of factors as specified by the min and max rule, then round to the nearest integer). |
demeantime | Demeans observations across time prior to component selection procedures, when “n=bn” or “n=ah”. |
sdizetime | Standardizes observations across time prior to component selection procedures, when “n=bn” or “n=ah”. |
demeancross | Demeans observations across cross-sections prior to component selection procedures, when “n=bn” or “n=ah”. |
sdizecross | Standardizes observations across cross-sections prior to component selection procedures, when “n=bn” or “n=ah”. |
PANIC VAR Lag Selection Options
For use when computing a PANIC test with
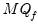
statistic.
varlagmethod=arg (default=“sic”) | Method for selecting lag length (number of first difference terms) to be included in the test statistic VAR: “aic” (Akaike), “sic” (Schwarz), “hqc” (Hannan-Quinn), “msaic” (Modified Akaike), “msic” (Modified Schwarz), “mhqc” (Modified Hannan-Quinn), “tstat” (Ng-Perron first backward significant t-statistic). |
varlag=integer | Use-specified fixed lag. |
varmaxlag=integer | Maximum lag length to consider when performing automatic lag length selection. Note: default is Schwert’s rule: let for 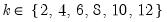 and let and let 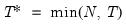 ; then the default maximum lag is given by ; then the default maximum lag is given by |
PANIC Long-run Variance Options
For use when computing a PANIC test using the
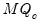
statistic.
Whitening Options
lag=arg | Lag specification: integer (user-specified number of lags), “a” (automatic selection). |
infosel=arg (default=“aic”) | Information criterion for automatic selection: “aic” (Akaike), “sic” (Schwarz), “hqc” (Hannan-Quinn) (if “lag=a”). |
maxlag=integer | Maximum lag-length for automatic selection (optional) (if “lag=a”). The default is an observation-based maximum of 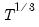 . |
Kernel Options
kern=arg (default=“bart”) | Kernel shape: “none” (no kernel), “bart” (Bartlett), “bohman” (Bohman), “daniell” (Daniel), “parzen” (Parzen), “parzriesz” (Parzen-Riesz), “parzgeo” (Parzen-Geometric), “parzcauchy” (Parzen-Cauchy), “quadspec” (Quadratic Spectral), “trunc” (Truncated), “thamm” (Tukey-Hamming), “thann” (Tukey-Hanning), “tparz” (Tukey-Parzen), “user” (User-specified; see “kernwgt=” below). |
kernwgt=vector | User-specified kernel weight vector (if “kern=user”). |
bw=arg (default=”nwfixed”) | Bandwidth: “fixednw” (Newey-West fixed), “andrews” (Andrews automatic), “neweywest” (Newey-West automatic), number (User-specified bandwidth). |
nwlag=integer | Newey-West lag-selection parameter for use in nonparametric bandwidth selection (if “bw=neweywest”). |
bwoffset=integer (default=0) | Apply integer offset to bandwidth chosen by automatic selection method (“bw=andrews” or “bw=neweywest”). |
bwint | Use integer portion of bandwidth chosen by automatic selection method (“bw=andrews” or “bw=neweywest”). |
PANIC p-value Options
mcreps=integer | Number of Monte Carlo replications. |
asymplen=integer | Asymptotic length of series. |
seed=number | Specifies the random number generator seed |
rng=arg | Specifies the type of random number generator. The key can be; improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4”) L’Ecuyer’s (1999) combined multiple, recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). |
Examples
grp.uroot2
The line above performs a PANIC unit root test on the series in the group GRP.
grp.uroot2(fsmethod=AH, mq=mqf, varlag=3)
The line above performs a PANIC unit root test using Ahn and Horenstein (2013) for factor selection determination and the
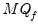
test for the number of common trends using a VAR(3) model.
grp.uroot2(test=cips, exog=trend, adnfosel=sic)
The line above performs a CIPS unit root test on the series in group GRP, with ADF testing performed on each cross-section with a constant and trend, and ADF lag selection using the Schwarz criterion.
Cross-references
See
“Unit Root Testing” for discussion of standard unit root tests performed on a single series, and
“Cross-sectionally Independent Panel Unit Root Testing” and
“Cross-sectionally Dependent Panel Unit Root Tests” for discussion of unit roots tests performed on panel structured workfiles, groups of series, or pooled data.
References
MacKinnon, James G., Alfred A. Haug, and Leo Michelis (1999), “Numerical Distribution Functions of Likelihood Ratio Tests For Cointegration,” Journal of Applied Econometrics, 14, 563-577.
Osterwald-Lenum, Michael (1992). “A Note with Quantiles of the Asymptotic Distribution of the Maximum Likelihood Cointegration Rank Test Statistics,” Oxford Bulletin of Economics and Statistics, 54, 461–472.
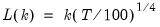
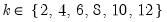 and let
and let 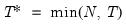 ; then the default maximum lag is given by
; then the default maximum lag is given by 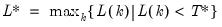
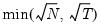
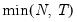 )
)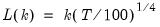
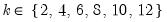 and let
and let 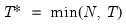 ; then the default maximum lag is given by
; then the default maximum lag is given by 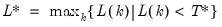
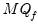 statistic.
statistic.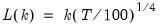
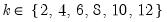 and let
and let 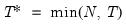 ; then the default maximum lag is given by
; then the default maximum lag is given by 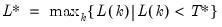
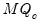 statistic.
statistic.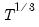 .
.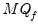 test for the number of common trends using a VAR(3) model.
test for the number of common trends using a VAR(3) model.