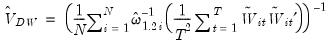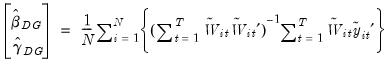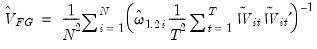Technical Details
Fully-Modified OLS
Phillips and Moon (1999), Pedroni (2000), and Kao and Chiang (2000) offer extensions of the Phillips and Hansen (1990) fully modified OLS estimator to panel settings.
Pooled FMOLS
The pooled FMOLS estimator outlined by Phillips and Moon (1999) is a straightforward extension of the standard Phillips and Hansen estimator. Given estimates of the average long-run covariances,
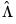
and
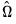
, we may define the modified dependent variable and serial correlation correction terms
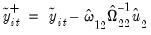 | (57.6) |
and
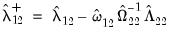 | (57.7) |
where
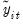
and
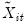
are the corresponding data purged of the individual deterministic trends, and
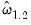
is the long-run average variance of
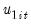
conditional on

. In the leading case of individual specific intercepts,
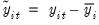
and
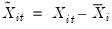
are the demeaned variables.
The pooled FMOLS estimator is then given by
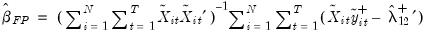 | (57.8) |
It is worth noting the pooled estimator simply sums across cross-sections separately in the numerator and denominator.
The estimates of the long-run covariances may be obtained by standard approaches using the
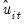
residuals obtained from estimating
Equation (57.1) and after removing the deterministic components in
Equation (57.2). Note that EViews allows you to relax the assumption of common
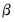
in these first stage estimates. Given estimates of the individual long-run covariances for each cross-section,
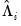
and
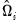
, we form our estimators by taking simple cross-section averages:
 | (57.9) |
Phillips and Moon (1999) show that under appropriate assumptions, the asymptotic distribution of the pooled estimator is asymptotically normal under sequential limits as
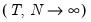
. Then
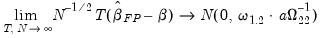 | (57.10) |
for a constant

that depends on the deterministic variable specification, where
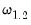
is the long-run variance of
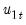
conditional on

, given by
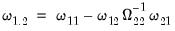
.
Instead of estimating the asymptotic variance directly using estimates of
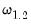
,
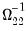
and the corresponding
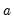
for every possible deterministic specification, EViews adopts the Pedroni (2000) and Mark and Sul (2003) approach of forming a consistent estimator using moments of the regressors:
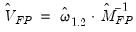 | (57.11) |
where
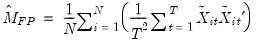 | (57.12) |
In related work, Mark and Sul (2003) propose a sandwich form of this estimator which allows for heterogeneous variances:
 | (57.13) |
where
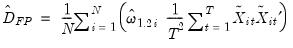 | (57.14) |
and the long-run variance estimates
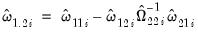
are computed for each cross-section. Note that degree-of-freedom corrections may be applied to the
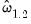
and

for comparability with standard regression standard error of the regression estimators.
Weighted FMOLS
Pedroni (2000) and Kao and Chiang (2000) describe feasible pooled FMOLS estimators for heterogeneous cointegrated panels where the long-run variances differ across cross-sections.
We again use first-stage estimates of the long-run and regressors equations to obtain the residuals, estimate the individual long-run variances
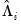
and
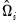
, and let
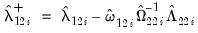 | (57.15) |
and
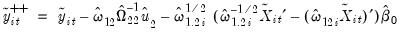 | (57.16) |
for
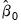
, a preliminary estimate of the long-run coefficient.
Next, we form the weighted variables:
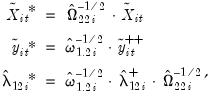 | (57.17) |
Then the estimator is given by
 | (57.18) |
and the asymptotic covariance is estimated using a moment estimator as in Pedroni (2000):
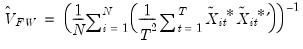 | (57.19) |
Group-Mean FMOLS
Pedroni (2000, 2001) proposes a grouped-mean FMOLS estimator which averages over the individual cross-section FMOLS estimates:
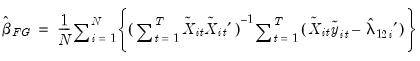 | (57.20) |
Pedroni (1990) notes that in the presence of heterogeneity in the cointegrating relationships, the grouped-mean estimator offers the desirable property of providing consistent estimates of the sample mean of the cointegrating vectors, in contrast to the pooled and weighted estimators.
We estimate the asymptotic covariance matrix for this estimator by computing the variance of the average of the individual estimates:
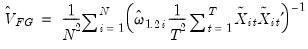 | (57.21) |
It is worth noting that the basic t-statistics obtained using this covariance estimator differ from the t-statistic proposed by Pedroni (1991), which aggregates individual statistics across the cross-section dimension.
Dynamic OLS (DOLS)
Kao and Chiang (2000), Mark and Sul (1999, 2003), and Pedroni (2001) propose extensions of the Saikkonen (1992) and Stock and Watson (1993) DOLS estimator to panel data settings. Panel DOLS involves augmenting the panel cointegrating regression equation with cross-section specific lags
and leads of
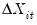
to eliminate the asymptotic endogenity and serial correlation.
Pooled DOLS
Kao and Chiang (2000) describe the pooled DOLS estimator in which we use ordinary least squares to estimate an augmented cointegrating regression equation:
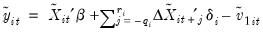 | (57.22) |
where
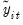
and
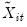
are the data purged of the individual deterministic trends. Note that the short-run dynamics coefficients

are allowed to be cross-section specific.
Let
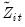
be regressors formed by interacting the
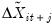
terms with cross-section dummy variables, and let
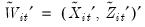
. Then the pooled DOLS estimator may be written as
 | (57.23) |
Kao and Chiang (2000) show that the asymptotic distribution of this estimator is the same as for pooled FMOLS. We may estimate the asymptotic covariance matrix of the
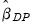
using the corresponding sub-matrix of:
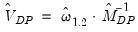 | (57.24) |
where
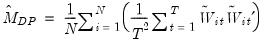 | (57.25) |
and
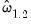
is an estimator of the long-run residual variance.
Alternately, Mark and Sul (2003) employ a sandwich estimator
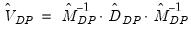 | (57.26) |
where
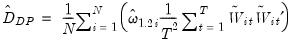 | (57.27) |
employs the individual long-run variance estimates
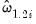
.
Weighted DOLS
Mark and Sul (1999) describe a simple weighted DOLS estimator which allows for heterogeneity in the long-run variances. Define the weighted regression:
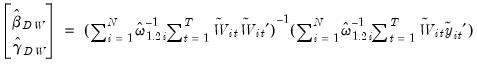 | (57.28) |
for individual long-run variance estimates
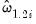
obtained after preliminary DOLS estimation.
In EViews, we estimate the asymptotic covariance matrix of the

using the corresponding sub-matrix of:
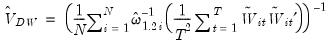 | (57.29) |
Note that this very simple form of weighted estimation differs from the more complex estimator described Kao and Chiang (2000), which mixes the FMOLS endogenity correction, weighting of both dependent variable and regressors, and the DOLS serial correlation correction.
Group-mean DOLS
Pedroni (2001) extends the grouped estimator concept to DOLS estimation by averaging over the individual cross-section DOLS estimates:
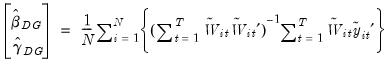 | (57.30) |
The asymptotic covariance matrix is obtained from the corresponding sub-matrix of the variance of the average of the individual estimators:
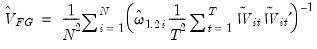 | (57.31) |
We again note that the basic t-statistics involving this covariance estimator differ from the t-statistic proposed by Pedroni (1991) which aggregates individual statistics across the cross-section dimension.
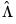 and
and 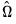 , we may define the modified dependent variable and serial correlation correction terms
, we may define the modified dependent variable and serial correlation correction terms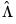 and
and 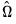 , we may define the modified dependent variable and serial correlation correction terms
, we may define the modified dependent variable and serial correlation correction terms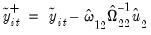
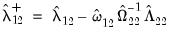
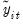 and
and 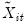 are the corresponding data purged of the individual deterministic trends, and
are the corresponding data purged of the individual deterministic trends, and 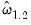 is the long-run average variance of
is the long-run average variance of 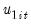 conditional on
conditional on  . In the leading case of individual specific intercepts,
. In the leading case of individual specific intercepts, 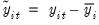 and
and 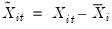 are the demeaned variables.
are the demeaned variables. 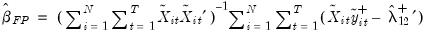
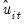 residuals obtained from estimating
residuals obtained from estimating
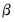 in these first stage estimates. Given estimates of the individual long-run covariances for each cross-section,
in these first stage estimates. Given estimates of the individual long-run covariances for each cross-section, 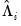 and
and 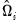 , we form our estimators by taking simple cross-section averages:
, we form our estimators by taking simple cross-section averages:
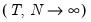 . Then
. Then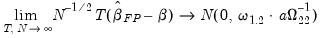
 that depends on the deterministic variable specification, where
that depends on the deterministic variable specification, where 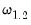 is the long-run variance of
is the long-run variance of 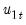 conditional on
conditional on  , given by
, given by 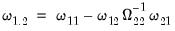 .
.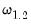 ,
, 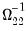 and the corresponding
and the corresponding 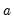 for every possible deterministic specification, EViews adopts the Pedroni (2000) and Mark and Sul (2003) approach of forming a consistent estimator using moments of the regressors:
for every possible deterministic specification, EViews adopts the Pedroni (2000) and Mark and Sul (2003) approach of forming a consistent estimator using moments of the regressors: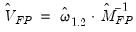
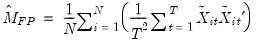

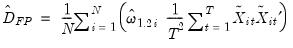
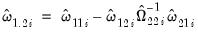 are computed for each cross-section. Note that degree-of-freedom corrections may be applied to the
are computed for each cross-section. Note that degree-of-freedom corrections may be applied to the 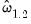 and
and  for comparability with standard regression standard error of the regression estimators.
for comparability with standard regression standard error of the regression estimators.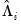 and
and 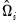 , and let
, and let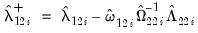
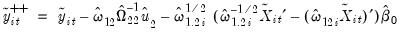
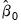 , a preliminary estimate of the long-run coefficient.
, a preliminary estimate of the long-run coefficient.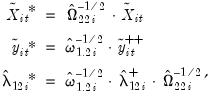

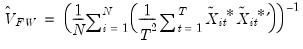
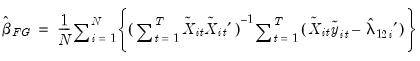
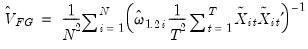
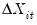 to eliminate the asymptotic endogenity and serial correlation.
to eliminate the asymptotic endogenity and serial correlation.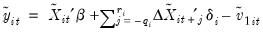
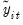 and
and 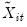 are the data purged of the individual deterministic trends. Note that the short-run dynamics coefficients
are the data purged of the individual deterministic trends. Note that the short-run dynamics coefficients  are allowed to be cross-section specific.
are allowed to be cross-section specific.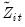 be regressors formed by interacting the
be regressors formed by interacting the 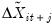 terms with cross-section dummy variables, and let
terms with cross-section dummy variables, and let 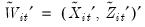 . Then the pooled DOLS estimator may be written as
. Then the pooled DOLS estimator may be written as
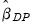 using the corresponding sub-matrix of:
using the corresponding sub-matrix of: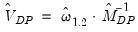
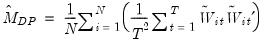
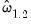 is an estimator of the long-run residual variance.
is an estimator of the long-run residual variance.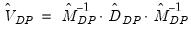
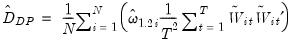
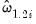 .
.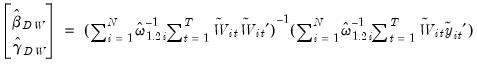
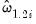 obtained after preliminary DOLS estimation.
obtained after preliminary DOLS estimation. using the corresponding sub-matrix of:
using the corresponding sub-matrix of: