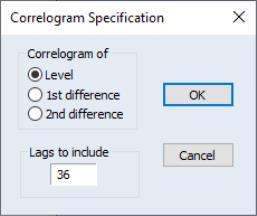

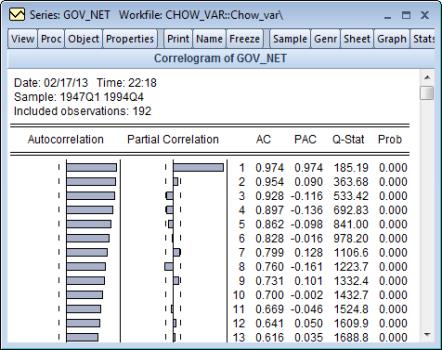
 at lag
at lag 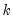 is estimated by:
is estimated by: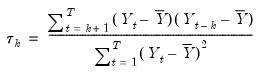 | (11.24) |
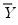 is the sample mean of
is the sample mean of 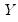 . This is the correlation coefficient for values of the series
. This is the correlation coefficient for values of the series 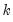 periods apart. If
periods apart. If 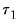 is nonzero, it means that the series is first order serially correlated. If
is nonzero, it means that the series is first order serially correlated. If 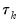 dies off more or less geometrically with increasing lag
dies off more or less geometrically with increasing lag 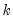 , it is a sign that the series obeys a low-order autoregressive (AR) process. If
, it is a sign that the series obeys a low-order autoregressive (AR) process. If 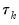 drops to zero after a small number of lags, it is a sign that the series obeys a low-order moving-average (MA) process. See
“Background” for a more complete description of AR and MA processes.
drops to zero after a small number of lags, it is a sign that the series obeys a low-order moving-average (MA) process. See
“Background” for a more complete description of AR and MA processes.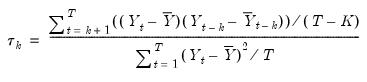 | (11.25) |
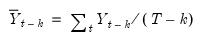 . The difference arises since, for computational simplicity, EViews employs the same overall sample mean
. The difference arises since, for computational simplicity, EViews employs the same overall sample mean 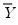 as the mean of both
as the mean of both 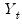 and
and 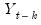 . While both formulations are consistent estimators, the EViews formulation biases the result toward zero in finite samples.
. While both formulations are consistent estimators, the EViews formulation biases the result toward zero in finite samples. . If the autocorrelation is within these bounds, it is not significantly different from zero at (approximately) the 5% significance level.
. If the autocorrelation is within these bounds, it is not significantly different from zero at (approximately) the 5% significance level. 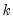 is the regression coefficient on
is the regression coefficient on 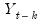 when
when 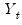 is regressed on a constant,
is regressed on a constant, 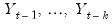 . This is a partial correlation since it measures the correlation of
. This is a partial correlation since it measures the correlation of  values that are
values that are 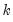 periods apart after removing the correlation from the intervening lags. If the pattern of autocorrelation is one that can be captured by an autoregression of order less than
periods apart after removing the correlation from the intervening lags. If the pattern of autocorrelation is one that can be captured by an autoregression of order less than 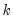 , then the partial autocorrelation at lag
, then the partial autocorrelation at lag 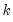 will be close to zero.
will be close to zero. , AR(
, AR(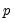 ), cuts off at lag
), cuts off at lag 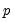 , while the PAC of a pure moving average (MA) process asymptotes gradually to zero.
, while the PAC of a pure moving average (MA) process asymptotes gradually to zero. 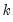 recursively by
recursively by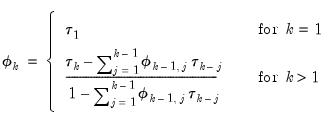 | (11.26) |
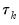 is the estimated autocorrelation at lag
is the estimated autocorrelation at lag 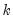 and where,
and where,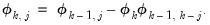 | (11.27) |
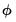 , simply run the regression:
, simply run the regression: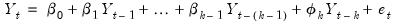 | (11.28) |
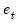 is a residual. The dotted lines in the plots of the partial autocorrelations are the approximate two standard error bounds computed as
is a residual. The dotted lines in the plots of the partial autocorrelations are the approximate two standard error bounds computed as 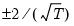 . If the partial autocorrelation is within these bounds, it is not significantly different from zero at (approximately) the 5% significance level.
. If the partial autocorrelation is within these bounds, it is not significantly different from zero at (approximately) the 5% significance level.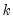 is a test statistic for the null hypothesis that there is no autocorrelation up to order
is a test statistic for the null hypothesis that there is no autocorrelation up to order 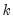 and is computed as:
and is computed as: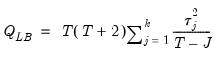 | (11.29) |
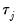 is the j-th autocorrelation and
is the j-th autocorrelation and 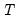 is the number of observations. If the series is not based upon the results of ARIMA estimation, then under the null hypothesis, Q is asymptotically distributed as a
is the number of observations. If the series is not based upon the results of ARIMA estimation, then under the null hypothesis, Q is asymptotically distributed as a 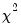 with degrees of freedom equal to the number of autocorrelations. If the series represents the residuals from ARIMA estimation, the appropriate degrees of freedom should be adjusted to represent the number of autocorrelations less the number of AR and MA terms previously estimated. Note also that some care should be taken in interpreting the results of a Ljung-Box test applied to the residuals from an ARMAX specification (see Dezhbaksh, 1990, for simulation evidence on the finite sample performance of the test in this setting).
with degrees of freedom equal to the number of autocorrelations. If the series represents the residuals from ARIMA estimation, the appropriate degrees of freedom should be adjusted to represent the number of autocorrelations less the number of AR and MA terms previously estimated. Note also that some care should be taken in interpreting the results of a Ljung-Box test applied to the residuals from an ARMAX specification (see Dezhbaksh, 1990, for simulation evidence on the finite sample performance of the test in this setting).