A linear state space representation of the dynamics of the 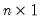 vector
vector 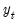 is given by the system of equations:
is given by the system of equations:
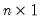 vector
vector 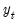 is given by the system of equations:
is given by the system of equations: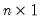 vector
vector 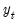 is given by the system of equations:
is given by the system of equations: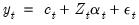 | (51.1) |
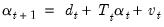 | (51.2) |
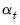 is an
is an 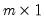 vector of possibly unobserved state variables, where
vector of possibly unobserved state variables, where 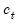 ,
, 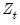 ,
, 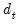 and
and 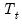 are conformable vectors and matrices, and where
are conformable vectors and matrices, and where 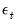 and
and 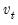 are vectors of mean zero, Gaussian disturbances. Note that the unobserved state vector is assumed to move over time as a first-order vector autoregression.
are vectors of mean zero, Gaussian disturbances. Note that the unobserved state vector is assumed to move over time as a first-order vector autoregression. 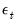 and
and 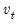 are assumed to be serially independent, with contemporaneous variance structure:
are assumed to be serially independent, with contemporaneous variance structure: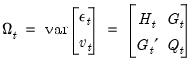 | (51.3) |
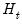 is an
is an 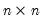 symmetric variance matrix,
symmetric variance matrix, 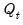 is an
is an 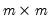 symmetric variance matrix, and
symmetric variance matrix, and 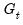 is an
is an 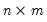 matrix of covariances.
matrix of covariances.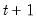 , given the errors specified in period
, given the errors specified in period  . This particular timing convention, which follows Koopman, Shephard, and Doornik (1999), has important implications for the interpretation of correlations between errors in the signal and state equations
. This particular timing convention, which follows Koopman, Shephard, and Doornik (1999), has important implications for the interpretation of correlations between errors in the signal and state equations 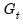 as discussed in
“A Note on Correlated Errors”.
as discussed in
“A Note on Correlated Errors”.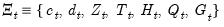 to depend upon observable explanatory variables
to depend upon observable explanatory variables 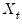 and unobservable parameters
and unobservable parameters 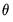 . Estimation of the parameters
. Estimation of the parameters 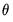 is discussed in
“Estimation”.
is discussed in
“Estimation”.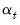 given information available at time
given information available at time 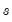 . We can define the mean and variance matrix of the conditional distribution as:
. We can define the mean and variance matrix of the conditional distribution as: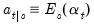 | (51.4) |
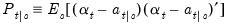 | (51.5) |
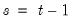 , so that we obtain the one-step ahead mean
, so that we obtain the one-step ahead mean 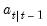 and one-step ahead variance
and one-step ahead variance 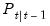 of the states
of the states 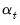 . Under the Gaussian error assumption,
. Under the Gaussian error assumption, 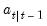 is also the minimum mean square error estimator of
is also the minimum mean square error estimator of 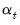 and
and 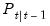 is the mean square error (MSE) of
is the mean square error (MSE) of 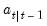 . If the normality assumption is dropped,
. If the normality assumption is dropped, 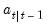 is still the minimum mean square linear estimator of
is still the minimum mean square linear estimator of 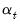 .
.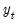 :
: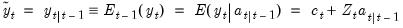 | (51.6) |
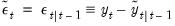 | (51.7) |
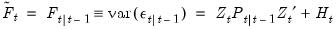 | (51.8) |
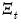 , and observations on
, and observations on 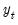 , the Kalman filter may be used to compute one-step ahead estimates of the state and the associated mean square error matrix,
, the Kalman filter may be used to compute one-step ahead estimates of the state and the associated mean square error matrix, 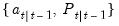 , the contemporaneous or filtered state mean and variance,
, the contemporaneous or filtered state mean and variance, 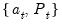 , and the one-step ahead prediction, prediction error, and prediction error variance,
, and the one-step ahead prediction, prediction error, and prediction error variance, 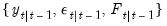 . Note that we may also obtain the standardized prediction residual,
. Note that we may also obtain the standardized prediction residual, 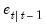 , by dividing
, by dividing 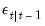 by the square-root of the corresponding diagonal element of
by the square-root of the corresponding diagonal element of 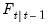 .
.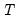 . The process of using this information to form expectations at any time period up to
. The process of using this information to form expectations at any time period up to 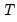 is known as fixed-interval smoothing. Despite the fact that there are a variety of other distinct forms of smoothing (e.g., fixed-point, fixed-lag), we will use the term smoothing to refer to fixed-interval smoothing.
is known as fixed-interval smoothing. Despite the fact that there are a variety of other distinct forms of smoothing (e.g., fixed-point, fixed-lag), we will use the term smoothing to refer to fixed-interval smoothing.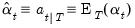 , and smoothed estimates of the state variances,
, and smoothed estimates of the state variances, 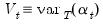 . The matrix
. The matrix 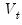 may also be interpreted as the MSE of the smoothed state estimate
may also be interpreted as the MSE of the smoothed state estimate 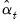 .
.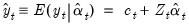 | (51.9) |
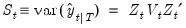 | (51.10) |
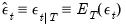 and
and 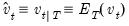 , and a corresponding smoothed disturbance variance matrix:
, and a corresponding smoothed disturbance variance matrix: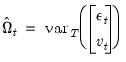 | (51.11) |
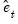 and
and 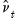 .
.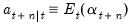 | (51.12) |
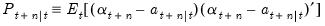 | (51.13) |
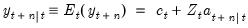 | (51.14) |
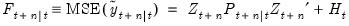 | (51.15) |
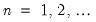 . As before,
. As before, 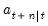 may also be interpreted as the minimum MSE estimate of
may also be interpreted as the minimum MSE estimate of 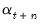 based on the information set available at time
based on the information set available at time 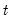 , and
, and 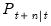 is the MSE of the estimate.
is the MSE of the estimate. 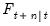 do not account for extra variability introduced in the estimation of any unknown parameters
do not account for extra variability introduced in the estimation of any unknown parameters 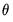 . In this setting, the
. In this setting, the 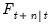 will understate the true variability of the forecast, and should be viewed as being computed conditional on the specific value of the estimated parameters.
will understate the true variability of the forecast, and should be viewed as being computed conditional on the specific value of the estimated parameters.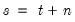 , simply initialize a Kalman filter at time
, simply initialize a Kalman filter at time 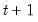 with the values of the predicted states and state covariances using information at time
with the values of the predicted states and state covariances using information at time 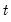 , and run the filter forward
, and run the filter forward 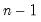 additional periods using no additional signal information. This procedure is repeated for each observation in the forecast sample,
additional periods using no additional signal information. This procedure is repeated for each observation in the forecast sample, 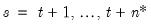 .
.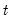 , and compute a complete set of n-period ahead forecasts for each period
, and compute a complete set of n-period ahead forecasts for each period 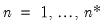 in the forecast interval. Thus, if we wish to start at period
in the forecast interval. Thus, if we wish to start at period 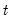 and forecast dynamically to
and forecast dynamically to 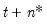 , we would compute a one-step ahead forecast for
, we would compute a one-step ahead forecast for 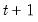 , a two-step ahead forecast for
, a two-step ahead forecast for 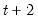 , and so forth, up to an
, and so forth, up to an 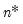 -step ahead forecast for
-step ahead forecast for 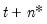 . It may be useful to note that as with n-step ahead forecasting, we simply initialize a Kalman filter at time
. It may be useful to note that as with n-step ahead forecasting, we simply initialize a Kalman filter at time 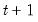 and run the filter forward additional periods using no additional signal information. For dynamic forecasting, however, only one n-step ahead forecast is required to compute all of the forecast values since the information set is not updated from the beginning of the forecast period.
and run the filter forward additional periods using no additional signal information. For dynamic forecasting, however, only one n-step ahead forecast is required to compute all of the forecast values since the information set is not updated from the beginning of the forecast period.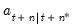 ). These forward looking forecasts may be computed by initializing the states at the start of the forecast period, and performing a Kalman smooth over the entire forecast period using all relevant signal data. This technique is useful in settings where information on the entire path of the signals is used to interpolate values throughout the forecast sample.
). These forward looking forecasts may be computed by initializing the states at the start of the forecast period, and performing a Kalman smooth over the entire forecast period using all relevant signal data. This technique is useful in settings where information on the entire path of the signals is used to interpolate values throughout the forecast sample.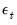 and
and 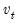 are Gaussian, the sample log likelihood:
are Gaussian, the sample log likelihood: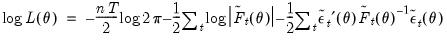 | (51.16) |
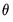 (see
Appendix C. “Estimation and Solution Options”).
(see
Appendix C. “Estimation and Solution Options”).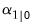 and variance matrix
and variance matrix 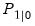 . With some stationary models, steady-state conditions allow us to use the system matrices to solve for the values of
. With some stationary models, steady-state conditions allow us to use the system matrices to solve for the values of 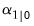 and
and 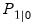 . In other cases, we may have preliminary estimates of
. In other cases, we may have preliminary estimates of 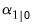 , along with measures of uncertainty about those estimates. But in many cases, we may have no information, or diffuse priors, about the initial conditions.
, along with measures of uncertainty about those estimates. But in many cases, we may have no information, or diffuse priors, about the initial conditions.