SVAR text restriction expressions involve linear equations or use a function-like syntax to specify restrictions on one or more matrix elements for the 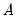 ,
, 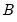 ,
, 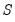 , and
, and 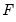 .
.
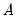 ,
, 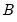 ,
, 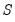 , and
, and 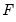 .
. append |
svar | Text for identifying restrictions for structural VAR. |
coint | Text for restrictions on the cointegration relations and/or adjustment coefficients. |
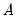 ,
, 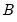 ,
, 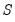 , and
, and 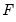 .
. 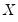 can be substituted with any of the canonical matrices
can be substituted with any of the canonical matrices 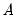 ,
, 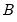 ,
, 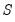 , and
, and 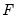 . The canonical names should not be preceded by “@” in this context since there is no potential workfile object ambiguity in the function argument(s).
. The canonical names should not be preceded by “@” in this context since there is no potential workfile object ambiguity in the function argument(s).@X = mat | Use mat as a pattern matrix for matrix X, e.g., “@a=mat1”, “@b = @mat2”. |
@vec(X)= 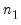 , , 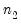 , , 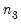 , ... , ... | Restricts all elements of matrix X similar using the specified pattern matrix (provided in list form). Element ordering matches the vectorization of the matrix, i.e., the elements of the first column, followed by the second column, followed by the third column, etc. |
@diag(X) | Restricts X to be a diagonal matrix, i.e., off-diagonal elements are zero. The diagonal elements are unrestricted. |
@diag(X) = n | Restricts X to be a diagonal matrix with elements on the diagonal restricted to be n. |
@lower(X) | Restricts X to be a lower triangular matrix, i.e., elements above the diagonal are zero. |
@unitlower(X) | Restricts X to be a unit lower triangular matrix, i.e., elements above the diagonal are zero and elements on the diagonal are one. |
@upper(X) | Restricts X to be an upper triangular matrix, i.e., elements below the diagonal are zero. |
@unitupper(X) | Restricts X to be a unit upper triangular matrix, i.e., elements below the diagonal are zero and elements on the diagonal are one. |
@row(X, r) = n | Restricts the elements in row r of X to equal n. |
@col(X, c) = n | Restricts the elements in column c of X equal n. |