Var
Vector autoregression and error correction object.
Var Declaration
var declare var estimation object.
To declare a var use the keyword var, followed by a name and, optionally, by an estimation specification:
var finvar
var empvar.ls 1 4 payroll hhold gdp
var finec.ec(e,2) 1 6 cp div r
Var Methods
btvcvar estimate a Bayesian time-varying coefficients VAR specification.
bvar estimate a Bayesian VAR specification.
ec estimate a vector error correction model.
ls estimate an unrestricted VAR.
mfvar mixed frequency VAR.
switchvar switching VAR (including simple and Markov switching).
Var Views
arlm serial correlation LM test.
arroots inverse roots of the AR polynomial.
coint Johansen cointegration test.
correl residual autocorrelations.
display display table, graph, or spool in object window.
endog table or graph of endogenous variables.
hdecomp perform historical decomposition for a standard VAR.
impulse impulse response functions.
jbera residual normality test.
label label information for the var object.
laglen lag order selection criteria.
output table of estimation results.
qstats residual portmanteau tests.
results table of estimation results.
rgmprobs display the regime probabilities in a switching VAR.
testexog exogeneity (Granger causality) tests.
transprobs display the state transition probabilities in a switching VAR.
white White heteroskedasticity test.
Var Procs
append append restriction text.
clearhist clear the contents of the history attribute.
copy creates a copy of the var.
drawcoefs draw from the posterior coefficient distribution.
drawrescov draw from the posterior error covariance distribution.
fit produce static forecasts from an estimated VAR.
forecast produce dynamic forecasts from an estimated VAR or VEC.
makecoefs create groups of the coefficient series used to make the BTVCVAR estimation output view.
makecoint make group of cointegrating relations.
makeess output effective sample sizes (ESSs) of the draws of the parameters in a BTVCVAR model.
makeif output inefficiency factors of the draws of the parameters in a BTVCVAR model.
makemodel make model from the estimated VAR or VEC.
makergmprobs save the regime probabilities from a switching VAR.
makerne output relative numerical efficiencies (RNEs) of the draws of the parameters in a BTVCVAR model.
maketransprobs save the state transition probabilities in a switching regression equation.
olepush push updates to OLE linked objects in open applications.
postdraws puts posterior draws of a BTVCVAR model in a new page.
setattr set the value of an object attribute.
svar estimate factorization matrix for structural innovations.
Var Data Members
Scalar Values (individual level data)
@eqlogl(k) log likelihood for equation k.
@eqncoef(k) number of estimated coefficients in equation k.
@eqregobs(k) number of observations in equation k.
@meandep(k) mean of the dependent variable in equation k.
@r2(k) R-squared statistic for equation k.
@rbar2(k) adjusted R-squared statistic for equation k.
@sddep(k) std. dev. of dependent variable in equation k.
@se(k) standard error of the regression in equation k.
@ssr(k) sum of squared residuals in equation k.
a(i,j) adjustment coefficient for the j-th cointegrating equation in the i-th equation of the VEC (where applicable).
b(i,j) coefficient of the j-th variable in the i-th cointegrating equation (where applicable).
c(i,j) coefficient of the j-th regressor in the i-th equation of the var, or the coefficient of the j-th first-difference regressor in the i-th equation of the VEC.
Scalar Values (system level data)
@aic Akaike information criterion for the system.
@detresid determinant of the residual covariance matrix.
@hq Hannan-Quinn information criterion for the system.
@lagcount number of lags included in the VAR.
@lagorder highest lag order included in the VAR.
@logl log likelihood for system.
@ncoefs total number of estimated coefficients in the var.
@neqn number of equations.
@nrestrict number of coefficient restrictions in the system.
@regobs number of observations in the var.
@sc Schwarz information criterion for the system.
@svarcvgtype integer indicating the convergence type of the structural decomposition estimation (structural VAR only): 0 (convergence achieved), 1 (convergence achieved, but first or second order conditions not met), 2 (failure to improve), 3 (maximum iterations reached), 4 (no convergence—structural decomposition not estimated).
@svaroverid over-identification LR statistic from structural factorization (structural VAR only).
@totalobs sum of @eqregobs from each equation (“@regobs*@neqn”).
Vectors and Matrices
@coefmat coefficient matrix (as displayed in output table).
@coefse matrix of coefficient standard errors (corresponding to the output table).
@cointadj matrix containing cointegrating variable adjustment coefficients
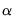
(where applicable).
@cointadjse matrix containing standard errors of cointegrating variable adjustment coefficients (where applicable).
@cointlr matrix containing long-run equilibrium coefficients
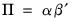
(where applicable).
@cointlrse matrix containing standard errors of long-run equilibrium coefficients (where applicable)
@cointse standard errors of matrix of cointegrating vectors (where applicable).
@cointsr matrix containing short-run adjustment coefficients
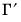
(where applicable).
@cointsrse matrix containing standard errors of short-run adjustment coefficients (where applicable).
@cointvec matrix of cointegrating vectors,
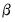
(where applicable).
@companion companion matrix for the full set of lag coefficients.
@impfact factorization matrix used in last impulse response view.
@lagcoefs coefficient matrix containing the full set of horizontally concatenated lag coefficient matrices.
@lagcoef(k) lag coefficient matrix for lag k.
@lagcoefsum sum of the lag coefficient matrices.
@lagids vector of integers containing the lags used in estimation.
@lrrsp accumulated long-run responses from last impulse response view.
@lrrspse standard errors of accumulated long-run responses.
@postresidcov estimated posterior error covariance for Bayesian models; ordinary residual covariance, otherwise.
@residcov (sym) covariance matrix of the residuals.
@svaramat estimated A matrix for structural factorization (structural VAR only).
@svarbmat estimated B matrix for structural factorization (structural VAR only).
@svarcovab covariance matrix of stacked A and B matrix for structural factorization (structural VAR only).
@svarfmat estimated F matrix for long-run impulse responses (structural VAR only).
@svarrcov restricted residual covariance matrix from structural factorization (structural VAR only).
@svarsmat estimated S matrix for short-run impulse responses (structural VAR only).
@swcompanion(i) switching companion matrix for the full set of lag coefficients in regime i (switching VAR only).
@swimpfact(i) switching factorization matrix for regime i used in last impulse response view (switching VAR only).
@swlagcoefs switching coefficient matrix containing the full set of horizontally concatenated lag coefficient matrices for regime i (switching VAR only).
@swlagcoefsum(i) sum of the switching lag coefficient matrices for regime i (switching VAR only).
String values
@attr("arg") string containing the value of the arg attribute, where the argument is specified as a quoted string.
@command full command line form of the estimation command. Note this is a combination of @method and @options.
@description string containing the VAR object’s description (if available).
@detailedtype returns a string with the object type: “VAR”.
@displayname returns the VAR’s display name. If the VAR has no display name set, the VAR’s name is returned.
@method command line form of the estimation method (“LS”, “BVAR”, etc.)
@name returns the VAR’s name.
@options command line form of estimation options.
@remarks string containing the var object’s remarks (if available).
@smpl sample used for estimation.
@type returns a string with the object type: “VAR”.
@updatetime returns a string representation of the time and date at which the VAR was last updated.
Var Examples
To declare a var estimate a VEC specification and make a residual series:
var finec.ec(e,2) 1 6 cp div r
finec.makeresids
To estimate an ordinary var, to create series containing residuals, and to form a model based upon the estimated var:
var empvar.ls 1 4 payroll hhold gdp
empvar.makeresids payres hholdres gdpres
empvar.makemodel(inmdl) cp fcp div fdiv r fr
To save coefficients in a scalar:
scalar coef1=empvar.b(1,2)
Append a specification line to a var.
Syntax
var_name.append(options) text
Type the text to be added after the append keyword. You must specify the restrictions type option.
Options
One of the following options is required when using append as a var proc:
svar | Text for identifying restrictions for structural VAR. |
coint | Text for restrictions on the cointegration relations and/or adjustment coefficients. |
VEC Restrictions
Restrictions may be placed on the coefficients B(r, k) of the r-th cointegrating relation and on the adjustment coefficients, where A(k, r) is the coefficient of the r-th cointegrating relation in the k-th VEC equation. Restrictions are entered in a comma separated list of the form:
B(r, k) = value
and
A(k, r) = value
SVAR Restrictions
SVAR text restriction expressions involve linear equations or use a function-like syntax to specify restrictions on one or more matrix elements for the
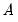
,
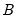
,
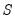
, and
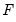
.
For direct restrictions on elements of the matrices, the EViews text syntax requires that the canonical structural matrix names are preceded by “@”, as in “@A”, or “@F”, to avoid ambiguity with workfile objects, e.g., scalars or matrix object elements.
EViews also offers function-like expressions that concisely specify popular sets of SVAR restrictions. In the following list, the token
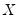
can be substituted with any of the canonical matrices
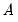
,
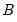
,
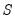
, and
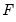
. The canonical names should not be preceded by “@” in this context since there is no potential workfile object ambiguity in the function argument(s).
@X = mat | Use mat as a pattern matrix for matrix X, e.g., “@a=mat1”, “@b = @mat2”. |
| Restricts all elements of matrix X similar using the specified pattern matrix (provided in list form). Element ordering matches the vectorization of the matrix, i.e., the elements of the first column, followed by the second column, followed by the third column, etc. |
@diag(X) | Restricts X to be a diagonal matrix, i.e., off-diagonal elements are zero. The diagonal elements are unrestricted. |
@diag(X) = n | Restricts X to be a diagonal matrix with elements on the diagonal restricted to be n. |
@lower(X) | Restricts X to be a lower triangular matrix, i.e., elements above the diagonal are zero. |
@unitlower(X) | Restricts X to be a unit lower triangular matrix, i.e., elements above the diagonal are zero and elements on the diagonal are one. |
@upper(X) | Restricts X to be an upper triangular matrix, i.e., elements below the diagonal are zero. |
@unitupper(X) | Restricts X to be a unit upper triangular matrix, i.e., elements below the diagonal are zero and elements on the diagonal are one. |
@row(X, r) = n | Restricts the elements in row r of X to equal n. |
@col(X, c) = n | Restricts the elements in column c of X equal n. |
Examples
var v
v.append(coint) b(1,1)=1
v.ec(restrict) 1 4 x y
First a VEC, V, is declared, then a restriction is appended to V, finally V is estimated with that restriction imposed.
var v
v.ls 1 3 y1 y2 y3
v.append(svar) @a(1,1) = 2.5
v.append(svar) @b(2,2) = @b(3,3) / 2
v.append(svar) @a(1,1) + @a(2,1) = 1
v.append(svar) @a(1,2) = 3 * @b(3,3)
v.append(svar) @s(1,1) + @s(2,2) - @f(3,3) = 1.5
v.svar
For an SVAR, we first estimate the VAR, then append restrictions then perform SVAR estimation.
Using a text expression equivalent to a pattern matrix:
v1.append(svar) @vec(s) = na, na, na, 0, na, na, 0, 0, na
v1.svar
Using a text expression with specialized function:
v1.append(svar) @lower(s)
v1.svar
Cross-references
Perform multivariate residual serial correlation LM test using an estimated Var.
Syntax
var_name.arlm(h, options)
You must specify the highest order of lag, h, for which to test.
Options
name=arg | Save LM statistics in named matrix object. The matrix has h rows and one column. |
prompt | Force the dialog to appear from within a program. |
p | Print test output. |
Examples
var var1.ls 1 6 lgdp lm1 lcpi
show var1.arlm(12,name=lmout)
The first line declares and estimates a VAR with 6 lags. The second line displays the serial correlation LM tests for lags up to 12 and stores the statistics in a matrix named LMOUT.
Cross-references
See
“Diagnostic Views” for other VAR diagnostics. See also
Var::qstats for related multivariate residual autocorrelation Portmanteau tests.
Inverse roots of the characteristic AR polynomial.
Syntax
var_name.arroots(options)
Options
name=arg | Save roots in named matrix object. Each root is saved in a row of the matrix, with the first column containing the real, and the second column containing the imaginary part of the root. |
graph | Plots the roots together with a unit circle. The VAR is stable if all of the roots are inside the unit circle. |
p | Print table of AR roots. |
Examples
var var1.ls 1 6 lgdp lm1 lcpi
var1.arroots(graph)
The first line declares and estimates a VAR with 6 lags. The second line plots the AR roots of the estimated VAR.
var var1.ls 1 6 lgdp lm1 lcpi
store roots
freeze(tab1) var1.arroots(name=roots)
The first line declares and estimates a VAR with 6 lags. The second line stores the roots in a matrix named ROOTS, and the table view as a table named TAB1.
Cross-references
See
“Diagnostic Views” for other VAR diagnostics.
Estimate a Bayesian time-varying coefficients VAR, or BTVCVAR, model.
Syntax
var_name.btvcvar(options) lag_pairs endog_list [@ exog_list]
btvcvar estimates a Bayesian time-varying coefficients VAR. The order of the VAR is specified using a lag pair, followed by a list of series or groups for endogenous variables. Exogenous variables can be included using the @-sign followed by a list of series or groups. A constant is automatically added to the list of exogenous variables; to estimate a specification without a constant, use the noconst option.
Options
Prior hyper-parameters
T0 = int (default = 0) | Set prior sample size 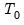 . A prior sample is not used if T0 is set to 0. To use a prior sample, T0 must be set to an integer larger than the number of coefficients per equation in a standard VAR version of the model. |
tau0 = num (default = 5.0) | Set prior scaling parameter for the initial state 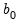 . |
tau1 = num (default = 1.0) | Set prior scaling parameter for the observation covariance 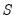 . |
nu1 = num (default = 5.0) | Set prior dof parameter for the observation covariance 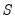 . |
tau2 = num (default = 0.01) | Set prior scaling parameter for the process covariance 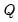 . |
nu2 = num (default = 5.0) | Set prior dof parameter for the process covariance 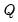 . |
Display options
usemean | Use posterior mean as the point estimate. The posterior median is used if usemean is not included in the options list. |
showci | Show credibility intervals (bands). |
cilevels = arg (default = "0.95") | Set credibility levels. For multiple levels, enter a space-delimited list of values surrounded by quotation marks, e.g., "0.3 0.5 0.8". |
uselines | Use lines instead of shading for credibility intervals. |
MCMC options
burn = int (default = 5000) | Set burn-in size. |
size = int (default = 5000) | Set posterior sample size. |
thin = int (default = 1) | Set thinning size. A thinning size of 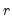 indicates that every 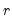 -th draw after the burn-in period is stored. |
nsub = int | Set the number of subchains. |
seed = int | Set the random seed. EViews will generate a seed if one is not specified. |
rng = arg (default = “kn” or method set via rndseed) | Set random number generator type. Available types are: improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4”), L’Ecuyer’s (1999) combined multiple recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). |
Other options
smoother = arg (default = "CFA") | Set simulation smoothing method. Available methods are "CFA" (Cholesky factor algorithm), "KFS" (Kalman filter and smoother), and "MMP" (McCausland, Miller, & Pelletier, 2011). |
stable | Use the method of Cogley & Sargent for obtaining stable draws. |
maxattempts = int (default = 100) | Set the maximum number of attempts for the sampler to draw stable VAR coefficients for all dates in the data sample. |
noconst | Do not include a constant in the exogenous regressors list. |
Examples
To declare and estimate a BTVCVAR named MYVAR with endogenous variables DGP and UNEMP, a constant, the first lag, and a prior sample of size 40, run
var myvar.btvcvar(t0=40) 1 1 gdp unemp
in the command window. Running the command
var myvar.btvcvar(t0=40, showci, cilevels="0.3 0.5") 1 1 gdp unemp
will also display shaded 30% and 50% credibility bands. For reproducible results, also set the number of subchains (nsub), the random seed (seed), and the random number generator type (rng):
var myvar.btvcvar(t0=40, nsub=12, seed=342458900, rng=kn, showci, cilevels="0.3 0.5") 1 1 gdp unemp
Command capture will always show the nsub, seed, and rng options.
Cross-references
Estimate a Bayesian VAR specification.
Syntax:
var_name.bvar(options) lag_pairs endog_list [@ exog_list]
bvar estimates an Bayesian VAR. You must specify the order of the VAR (using one or more pairs of lag intervals), and then provide a list of series or groups to be used as endogenous variables. You may include exogenous variables such as trends and seasonal dummies in the VAR by including an “@-sign” followed by a list of series or groups. A constant is automatically added to the list of exogenous variables; to estimate a specification without a constant, you should use the option “noconst”.
Options
General options
noconst | Do not include a constant in exogenous regressors list. |
prior = keyword (default= “lit”) | Set the prior type: “lit” (Litterman/Minnesota), “nw” (Normal-Wishart), “sznw” (Sims-Zha Normal-Wishart prior), “sznf” (Sims-Zha Normal-flat prior), “glp” (Giannone, Lenze, and Primiceri). |
initcov = keyword (default = “uni”) | Set the (initial) residual variance-covariance: “full” (full Classical VAR), “uni” (univariate AR), “diag” (diagonal of full classical VAR), “arconst” (univariate AR and a constant) By default, EViews uses the “initcov=uni” option so that diagonal elements of the prior residual variance-covariance can be obtained from the estimation of a set of univariate AR models. |
nodf | Do not degree-of-freedom correct the initial residual covariance. |
initexog | Use exogenous variables in initial covariance estimate. |
initdummied | Use dummy variables in initial covariance estimate. (Only applicable if dummy variable options are below). |
icsmpl = arg | Set the sample used for initial covariance estimate (estimation sample used if omitted). |
sumcoef | Use the sum-of-coefficients dummy variable (only applicable if not using Sims-Zha or GLP prior). |
initobs | Use the initial-observations dummy variable (only applicable if not using Sims-Zha or GLP prior). |
nsumcoef | Do not use sum-of-coefficients dummy variable (only applicable if using Sims-Zha or GLP prior). |
ninitobs | Do not use initial-observations dummy variable (only applicable if using Sims-Zha or GLP prior). |
l0 = num | Set the residual covariance tightness hyper-parameter. |
l1 = num | Set the overall tightness hyper-parameter. |
l2 = num | Set the relative cross-variable weight hyper-parameter. |
l3 = num | Set the lag decay hyper-parameter. |
l4 = num | Set the exogenous variables hyper-parameter. |
l5 = num | Set the other exogenous variables hyper-parameter. |
mu1 = num | Set the AR(1) coefficient dummies hyper-parameter. |
mu5 = num | Set the sum of coefficient dummies hyper-parameter. |
mu6 = num | Set the initial observation dummies hyper-parameter. |
c1 = num | Set the S scale hyper-parameter. |
c2 = num | Set the V scale hyper-parameter. |
c3 = num | Set the degrees-of-freedom hyper-parameter. |
optl1 | Optimize the L1 hyper-parameter. |
optl3 | Optimize the L3 hyper-parameter. |
optmu5 | Optimize the MU5 hyper-parameter. |
optmu6 | Optimize the MU6 hyper-parameter. |
optpsi | Optimize the initial covariance estimates. |
draws = num | Set the number of MCMC draws (only applicable with “prior=inw”). |
seed = num | Set the seed for the MCMC generator (only applicable with “prior=inw”). |
burn = num | Set the percentage of MCMC draws to use as a burn-in (only applicable with “prior=inw”). |
m=integer | Set maximum number of iterations (only applicable with “prior=glp”). |
c=scalar | Set convergence criterion (only applicable with “prior=glp”). |
prompt | Force the dialog to appear from within a program. |
p | Print basic estimation results. |
Examples
var mvar.bvar 1 3 m1 gdp
declares and estimates an Bayesian VAR with a Litterman prior named MVAR with two endogenous variables (M1 and GDP), a constant and 3 lags (1 through 3).
mvar.bvar(noconst) 1 3 ml gdp
estimates the same VAR, but with no constant.
var mvar.bvar(prior=nw, mu1=0.2, C1=0.2) 1 3 m1 gdp
specifies a normal-Wishart with hyper-prior values specified as mu1=0.2, C1=0.2.
var mvar.bvar(prior=inw, c1=0.15,c2=0.15, draws=50000) 1 3 m1 gdp
specifies an independent normal-Wishart prior with both C1 and C2 hyper-parameters set equal to 0.15, and the number of Gibb’s sampler draws set to 50,000.
Var mbvar.bvar(prior=glp, initcov=diag, nsumcoef, ninitobs, optl3, m=5000) 1 3 m1 gdp
Specifies a Giannone-Lenza-Primeceri prior, where only Lambda 3 will be optimized, the initial covariance matrix is estimated as a diagonal VAR, neither initial dummy observation priors, and the number of optimization iterations set to 5,000.
Cross-references
See also
Var::ls and
Var::ec for estimation of ordinary VARs and error correction models.
Clear the contents of the history attribute for VAR objects.
Removes the VAR’s history attribute, as shown in the label view of the VAR.
Syntax
var_name.clearhist
Examples
v1.clearhist
v1.label
The first line removes the history from the VAR V1, and the second line displays the label view of V1, including the now blank history field.
Cross-references
See
“Labeling Objects” for a discussion of labels and display names.
Clear the contents of the remarks attribute.
Removes the var’s remarks attribute, as shown in the label view of the var.
Syntax
var_name.clearremarks
Examples
v1.clearremarks
v1.label
The first line removes the remarks from the var V1, and the second line displays the label view of V1, including the now blank remarks field.
Cross-references
See
“Labeling Objects” for a discussion of labels and display names.
Clear restriction text from a VAR object.
Syntax
var_name.cleartext(arg)
You must specify the text type you wish to clear using one of the following arguments:
svar | Clear text of identifying restrictions for a structural VAR. |
coint | Clear text of restrictions on the cointegration relations and/or adjustment coefficients. |
Examples
var1.cleartext(svar)
var1.append(svar) @lr2(@u1) = 0
The first line clears the structural VAR identifying restrictions in VAR1. The next line specifies a new long-run restriction for a structural factorization.
Cross-references
Johansen’s cointegration test for the series in the var object.
Syntax
var_name.coint(options) [lag_spec] [@ x1 x2 x3 ...] [@exogsr sx1 sx2 sx3 ...] [@exoglr lx1 lx2 lx3 ...] [@exogboth bx1 bx2 bx3 ...]
uses the coint keyword followed by options, and optionally,
• a lag_spec consisting of one or more pairs of lag intervals, where the lag orders are for the differences in the error correction representation of the VEC, not the levels representation of the VAR.
• an “@”-sign or “@exogsr” followed by a list of exogenous variables in the short-run equation only
• “@exoglr” followed by a list of exogenous variables in the long-run relation only
• “@exogboth” followed by a list of exogenous variables in both the long-run relation and the short-run equations
The coint command tests for cointegration among the series in the var object using the lag spec, exogenous variables, and if relevant, deterministic spec and VEC restrictions specified in estimation.
• You may provide explicit lag_spec to override the one used in estimation.
Note that if the estimation lags were for a VAR specification in levels, the default lag_spec will be the original spec adjusted for the error correction differences. Thus, if the original estimation was for a “1 4” VAR, the default lag_spec will be “1 3”.
• You may provide a “determ=” option to override an existing VEC deterministic trend specification.
• You may explicitly list any type of exogenous variable to override the entire existing specification for the exogenous variables.
The output for cointegration tests displays p-values for the rank test statistics. These p-values are computed using the response surface coefficients as estimated in MacKinnon, Haug, and Michelis (1999). The 0.05 critical values are also based on the response surface coefficients from MacKinnon-Haug-Michelis. Note: the reported critical values assume no exogenous variables other than an intercept and trend.
Options
Deterministic Trend Option
There are 8 different deterministic trend assumptions that you may specify using the “determ=arg” option.
These cases correspond to whether the intercept (“c”) and the trend (“t”) are either
• not included (“n”)
• in the long-run cointegrating relation only (“l”)
• in the short-run equation only (“s”)
• in both the long and short-run equations (“b”)
The values of arg are text shortcuts formed by joining a text shortcut for the intercept specification with a text shortcut for the trend specification.
The individual intercept and trend specifications are formed by joining the “c” and the “t” with the appropriate letter describing inclusion in the long and short-run equations.
For example,
• “cb” indicates that the constant is in both the long and short-run equation
• “tl” indicates that the trend is in the long-run cointegrating equation only
so that
• “cbtl” indicates that the constant is in both the long and short-run and the trend is in the long-run only
Using this convention (along with a special “none” option), we may easily describe options arguments for all 8 deterministic cases:
cntn, none | Case 1: No deterministic terms. Corresponding VAR model has no deterministic terms. |
cltn | Case 2: Restricted constant. Constant only in the cointegrating relations. Corresponding VAR has a constant. |
cbtn (default) | Case 3 (JHJ): Unrestricted constant Constant included both in the short-run equation and (artificially) in the cointegrating relations via orthogonalization. Corresponding VAR has a constant and trend. |
cstn | Case 3: Unrestricted constant Constant only in the short-run equation. Corresponding VAR has a trend. |
cbtl | Case 4 (JHJ): Unrestricted constant and restricted trend Constant included both in the short-run equation and (artificially) in the cointegrating relations via orthogonalization, and trend included only in the cointegrating relations. Corresponding VAR has a constant and trend. |
cstl | Case 4: Unrestricted constant and restricted trend Constant only in the short-run equation, and trend only in the cointegrating relation. Corresponding VAR has a trend. |
cbtb | Case 5 (JHJ): Unrestricted constant and trend Constant and trend both included in the short-run equation and (artificially) in the cointegrating relations via orthogonalization. Corresponding VAR has a constant, linear, and quadratic trend. |
csts | Case 5: Unrestricted constant and trend Constant and trend both included in the short-run equation. Corresponding VAR has a linear and quadratic trend. |
or you may use the “determsummary” option to compute tests under all deterministic assumptions.
Other Options
determsummary | Summarize all deterministic trend cases. |
restrict | Impose restrictions as specified by the
Var::append proc, or the “restspec=” option. |
restspec="spec" | Define the restricted VEC specification where spec is a space a space delimited list of VEC coefficient restrictions. |
m = integer, maxit = integer | Maximum number of iterations for restricted estimation (only valid if you choose the restrict option). |
c = scalar, cvg = scalar | Convergence criterion for restricted estimation. (only valid if you choose the restrict option). |
save = mat_name | Stores test statistics as a named matrix object. The save= option stores a 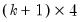 matrix, where 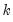 is the number of endogenous variables in the VAR. The first column contains the eigenvalues, the second column contains the maximum eigenvalue statistics, the third column contains the trace statistics, and the fourth column contains the log likelihood values. The i-th row of columns 2 and 3 are the test statistics for rank 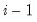 . The last row is filled with NAs, except the last column which contains the log likelihood value of the unrestricted (full rank) model. |
cvtype=ol | Display 0.05 and 0.01 critical values from Osterwald-Lenum (1992). This option reproduces the output from version 4. The default is to display critical values based on the response surface coefficients from MacKinnon-Haug-Michelis (1999). Note that the argument on the right side of the equals sign are letters, not numbers 0-1). |
cvsize=arg (default=0.05) | Specify the size of MacKinnon-Haug-Michelis (1999) critical values to be displayed. The size must be between 0.0001 and 0.9999; values outside this range will be reset to the default value of 0.05. This option is ignored if you set “cvtype=ol”. |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Examples
var1.coint(determ=cbtl) 1 12 @
carries out the Johansen test for the series in the var object named VAR1 using lags 1 to 12. The “@”-sign without a list of exogenous variables ensures that the test does not include any exogenous variables in VAR1.
Cross-references
See
“Johansen Cointegration Test” for details on the Johansen test.
Creates a copy of the var.
Creates either a named or unnamed copy of the var.
Syntax
var_name.copy
var_name.copy dest_name
Examples
v1.copy
creates an unnamed copy of the var V1.
v1.copy v2
creates V2, a copy of the var V1.
Cross-references
Display autocorrelation and partial correlations.
Displays the autocorrelation and partial correlation functions in the specified form, together with the Q-statistics and p-values associated with each lag.
Syntax
var_name.correl(n, options)
You must specify the largest lag n to use when computing the autocorrelations.
Options
graph (default) | Display correlograms (graphs). |
byser | Display autocorrelations in tabular form, by series. |
bylag | Display autocorrelations in tabular form, by lag. |
name=arg | Saves matrix of results containing the data corresponding to the specified view. |
prompt | Force the dialog to appear from within a program. |
p | Print the correlograms. |
Examples
v1.correl(24, byser)
Displays the correlograms of V1 in tabular form by series, for up to 24 lags.
Cross-references
See
“Autocorrelations (AC)” and
“Partial Autocorrelations (PAC)” for a discussion of autocorrelation and partial correlation functions, respectively.
Display table, graph, or spool output in the VAR object window.
Display the contents of a table, graph, or spool in the window of the VAR object.
Syntax
var_name.display object_name
Examples
var1.display tab1
Display the contents of the table TAB1 in the window of the object VAR1.
Cross-references
Most often used in constructing an EViews Add-in. See
“Custom Object Output”.
Display name for a var object.
Attaches a display name to a var object which may be used to label output in place of the standard var object name.
Syntax
var_name.displayname display_name
Display names are case-sensitive, and may contain a variety of characters, such as spaces, that are not allowed in var object names.
Examples
hrs.displayname Hours Worked
hrs.label
The first line attaches a display name “Hours Worked” to the var object HRS, and the second line displays the label view of HRS, including its display name.
Cross-references
See
“Labeling Objects” for a discussion of labels and display names.
Estimate a vector error correction model (VEC).
Syntax
var_name.ec(options) lag_pairs endog_list [@ x1 x2 x3 ...] [@exogsr sx1 sx2 sx3 ...] [@exoglr lx1 lx2 lx3 ...] [@exogboth bx1 bx2 bx3 ...]
Specify the order of the VEC by entering lag_pairs consisting of one or more pairs of lag intervals, and then list the series or groups to be used as endogenous variables.
Note that the lag orders are for the differences in the error correction representation of the VEC, not the levels representation of the VAR. If you are comparing results obtained elsewhere, you should be certain that the specifications for the lag orders are comparable.
In addition, you may optionally provide:
• an “@”-sign or “@exogsr” followed by a list of exogenous variables in the short-run equation only
• “@exoglr” followed by a list of exogenous variables in the long-run relation only
• “@exogboth” followed by a list of exogenous variables in both the long-run relation and the short-run equations
Do not include an intercept or trend in the VEC specification, these deterministic trend terms should be specified using the “determ=” option, as described below.
Options
Deterministic Trend Option
There are 8 different deterministic trend assumptions that you may specify using the “determ=arg” option.
These cases correspond to whether the intercept (“c”) and the trend (“t”) are either
• not included (“n”)
• in the long-run cointegrating relation only (“l”)
• in the short-run equation only (“s”)
• in both the long and short-run equations (“b”)
The values of arg are text shortcuts formed by joining a text shortcut for the intercept specification with a text shortcut for the trend specification.
The individual intercept and trend specifications are formed by joining the “c” and the “t” with the appropriate letter describing inclusion in the long and short-run equations.
For example,
• “cb” indicates that the constant is in both the long and short-run equation
• “tl” indicates that the trend is in the long-run cointegrating equation only
so that
• “cbtl” indicates that the constant is in both the long and short-run and the trend is in the long-run only
Using this convention (along with a special “none” option), we may easily describe options arguments for all 8 deterministic cases:
cntn, none | Case 1: No deterministic terms. Corresponding VAR model has no deterministic terms. |
cltn | Case 2: Restricted constant. Constant only in the cointegrating relations. Corresponding VAR has a constant. |
cbtn (default) | Case 3 (JHJ): Unrestricted constant Constant included both in the short-run equation and (artificially) in the cointegrating relations via orthogonalization. Corresponding VAR has a constant and trend. |
cstn | Case 3: Unrestricted constant Constant only in the short-run equation. Corresponding VAR has a trend. |
cbtl | Case 4 (JHJ): Unrestricted constant and restricted trend Constant included both in the short-run equation and (artificially) in the cointegrating relations via orthogonalization, and trend included only in the cointegrating relations. Corresponding VAR has a constant and trend. |
cstl | Case 4: Unrestricted constant and restricted trend Constant only in the short-run equation, and trend only in the cointegrating relation. Corresponding VAR has a trend. |
cbtb | Case 5 (JHJ): Unrestricted constant and trend Constant and trend both included in the short-run equation and (artificially) in the cointegrating relations via orthogonalization. Corresponding VAR has a constant, linear, and quadratic trend. |
csts | Case 5: Unrestricted constant and trend Constant and trend both included in the short-run equation. Corresponding VAR has a linear and quadratic trend. |
Other Options
rank = integer (default = 1) | Number of cointegrating relationships. |
restrict | Impose restrictions as specified by the
Var::append proc, or the “restspec=” option. |
restspec="spec" | Define the restricted VEC specification where spec is a space a space delimited list of VEC coefficient restrictions. |
m = integer, maxit = integer | Maximum number of iterations for restricted estimation (only valid if you choose the restrict option). |
c = scalar, cvg = scalar | Convergence criterion for restricted estimation. (only valid if you choose the restrict option). |
prompt | Force the dialog to appear from within a program. |
p | Print the results view. |
Examples
var macro1.ec 1 4 m1 gdp tb3
declares a var object MACRO1 and estimates a VEC with four lagged first differences, three endogenous variables and one cointegrating equation using the default trend option “c”.
var term.ec(determ=cstl, rank=2) 1 2 4 4 tb1 tb3 tb6 @ d2 d3 d4
declares a var object TERM and estimates a VEC with lagged first differences of order 1, 2, 4, three endogenous variables, three exogenous variables, and two cointegrating equations using deterministic trend option “determ=cstl” for a model with a constant in the short-run equation, and a trend in the long-run cointegrating relation.
var macro1.ec(determ=cstl, rank=2) 1 2 4 4 tb1 tb3 tb6 @exogsr exog1 @exoglr exog2 @exogdual exog3
The line above declares a VAR object MACRO01 with the same basic specification as TERM, but with an additional short-run exogenous variable EXOG1, a long-run exogenous variable EXOG2, and a dual exogenous variable EXOG3.
Cross-references
See
Var::ls and
Var::bvar for estimation of ordinary VARs and Bayesian VAR models. See also
Var::coint and
Var::append.
Draw from the posterior coefficient distribution.
Draws samples from the posterior coefficient distribution of a Bayesian VAR and saves the individual draws into a matrix object. Each row of the matrix will contain the vec’d coefficients from a single draw.
Syntax
var_name.drawcoefs(options) matrix_name
Options
draws=integer (default=1000) | Number of draws. |
burn=arg (default=0.1) | Proportion of initial draws to discard (only applicable if Bayesian VAR was estimated with “prior=inw”) |
seed=integer | Random number seed. |
Examples
var1.drawcoefs(draws=10000) vardraws
will create a matrix object, VARDRAWS, with 10,000 rows, containing draws from the posterior coefficient distribution.
Cross-references
See
“Bayesian VAR Models” for details on drawing from the posterior distributions.
Draw from the posterior coefficient distribution.
Draws samples from the posterior residual covariance distribution of a Bayesian VAR and saves the individual draws into a matrix object. Each row of the matrix will contain the vec’d form of the covariance matrix from a single draw.
Syntax
var_name.drawrescov(options) matrix_name
Options
draws=integer (default=1000) | Number of draws. |
burn=arg (default=0.1) | Proportion of initial draws to discard (only applicable if Bayesian VAR was estimated with “prior=inw”) |
seed=integer | Random number seed. |
Examples
var1.drawrescov(draws=10000) vardraws
will create a matrix object, VARDRAWS, with 10,000 rows, containing draws from the posterior residual covariance distribution.
Cross-references
See
“Bayesian VAR Models” for details on drawing from the posterior distributions.
Displays a spreadsheet or graph view of the endogenous variables.
Syntax
var_name.endog(options)
Options
g | Multiple line graphs of the solved endogenous series. |
p | Print the table of solved endogenous series. |
Examples
var1.endog(g,p)
prints the graphs of the solved endogenous series.
Cross-references
Computes static forecasts of the VAR or VEC equation.
fit computes the static forecast of variables and all observations in a specified sample. In some settings, you may instruct forecast to compare the forecasted data to actual data, and to compute summary statistics.
Syntax
var_name.fit(options) f_pattern [se_pattern]
You should enter a naming suffix for the forecast series and, optionally, a naming suffix for the series containing the standard errors. Standard errors are currently only available for non-Bayesian VARs, and are computed via simulation.
Not currently available for switching VARs
Options
General Options
g | Graph the forecasts in individual graphs - one per dependent variable. |
m | Graph the forecasts in a combined graph. |
e | Produce the forecast evaluation table. |
f = arg (default= “actual”) | Out-of-forecast-sample fill behavior: “actual” (fill observations outside the forecast sample with actual values for the fitted variable), “na” (fill observations outside the forecast sample with missing values). |
prompt | Force the dialog to appear from within a program. |
p | Print view. |
Non-Bayesian Options
streps=integer | Number of simulation repetitions. Only applicable if a se_pattern is provided. |
f=number | Fraction of failed repetitions before stopping. Only applicable if a se_pattern is provided. |
BVAR Options
classical | Perform classical forecasting – forecast based upon the posterior means of the coefficients as if they were calculated from a classical VAR. If omitted Bayesian sampling is used. |
If “classical” is not specified, the following Bayesian forecasting options are available:
mean | Store the mean of the draws from the sampler. If omitted the median is stored. |
draws=integer (default= 100000) | Number of draws. |
burn=arg (default=0.1) | Proportion of initial draws to discard. |
seed=integer | Random number seed. |
dropunstable | Drop any draws that produce unstable coefficients. |
dgraph | Produce distribution graphs. |
fangraph | Produce fan graphs. |
page=arg | Store the individual draws in a new page. |
BTVCVAR Options
usemean | Use posterior mean as the point estimate. The posterior median is used if usemean is not included in the options list. |
showci | Show credibility intervals (bands). |
cilevels = arg (default = "0.95") | Set credibility levels. For multiple levels, enter a space-delimited list of values surrounded by quotation marks, e.g., "0.3 0.5 0.8". |
uselines | Use lines instead of shading for credibility intervals. |
seed = int | Set the random seed. EViews will generate a seed if one is not specified. |
rng = arg (default = “kn” or method set via rndseed) | Set random number generator type. Available types are: improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4”), L’Ecuyer’s (1999) combined multiple recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). |
Examples
The following lines:
smpl 1970q1 1990q4
var var1.ls 1 3 con inc
smpl 1991q1 1995q4
var1.fit(m) _f _se
estimate a VAR over the period 1970Q1–1990Q4, and then computes static forecasts for the period 1991Q1–1995Q4, and plots the forecasts as line graphs.
Cross-references
See
“Forecasting” for a discussion of forecasting from VARs.
Computes (n-period ahead) dynamic forecasts of the VAR or VEC equation.
forecast computes the forecast for all variables and all observations in a specified sample. In some settings, you may instruct forecast to compare the forecasted data to actual data, and to compute summary statistics.
Syntax
var_name.forecast(options) f_pattern [se_pattern]
You should enter a naming suffix for the forecast series and, optionally, a naming suffix for the series containing the standard errors. Forecast standard errors are currently only available for non-Bayesian VARs, and are computed via simulation.
Not currently available for switching VARs
Options
General Options
g | Graph the forecasts in individual graphs - one per dependent variable. |
m | Graph the forecasts in a combined graph. |
e | Produce the forecast evaluation table. |
f = arg (default= “actual”) | Out-of-forecast-sample fill behavior: “actual” (fill observations outside the forecast sample with actual values for the fitted variable), “na” (fill observations outside the forecast sample with missing values). |
prompt | Force the dialog to appear from within a program. |
p | Print view. |
Non-Bayesian Options
streps=integer | Number of simulation repetitions. Only applicable if a se_pattern is provided. |
f=number | Fraction of failed repetitions before stopping. Only applicable if a se_pattern is provided. |
BVAR Options
classical | Perform classical forecasting – forecast based upon the posterior means of the coefficients as if they were calculated from a classical VAR. If omitted Bayesian sampling is used. |
If “classical” is not specified, the following Bayesian forecasting options are available:
mean | Store the mean of the draws from the sampler. If omitted the median is stored. |
draws=integer (default= 100000) | Number of draws. |
burn=arg (default=0.1) | Proportion of initial draws to discard. |
seed=integer | Random number seed. |
dropunstable | Drop any draws that produce unstable coefficients. |
dgraph | Produce distribution graphs. |
fangraph | Produce fan graphs. |
page=arg | Store the individual draws in a new page. |
BTVCVAR Options
usemean | Use posterior mean as the point estimate. The posterior median is used if usemean is not included in the options list. |
showci | Show credibility intervals (bands). |
cilevels = arg (default = "0.95") | Set credibility levels. For multiple levels, enter a space-delimited list of values surrounded by quotation marks, e.g., "0.3 0.5 0.8". |
uselines | Use lines instead of shading for credibility intervals. |
seed = int | Set the random seed. EViews will generate a seed if one is not specified. |
rng = arg (default = “kn” or method set via rndseed) | Set random number generator type. Available types are: improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4”), L’Ecuyer’s (1999) combined multiple recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). |
Examples
The following lines:
smpl 1970q1 1990q4
var var1.ls 1 3 con inc
smpl 1991q1 1995q4
var1.forecast(m) _f _se
estimate a VAR over the period 1970Q1–1990Q4, and then computes dynamic forecasts for the period 1991Q1–1995Q4, and plots the forecasts as line graphs.
smpl 1970q1 1990q4
var var2.bvar(prior=inw) 1 3 con inc
smpl 1991q1 1995q4
var1.forecast(m, draws=50000, burn=.05, dgraph, page=draws) _f
estimates a Bayesian VAR with an independent normal-Wishart prior over the same period, and then forecasts that VAR taking 50,000 draws of a Gibbs sampler, discarding the first 2,500 draws, producing a distribution graph of the forecasts and storing the draws into a new panel page called DRAWS.
Cross-references
See
“Forecasting” for a discussion of forecasting from VARs and VECS.
Performs graph of historical decomposition for a standard VAR.
Syntax
var_name.hdecomp(n, options) [ser1 ser2 ser3 ...] [@ component_series [@ ordering_series]]
List the series names in the Var you would like to decompose in the order you wish to display the graphs. If you do not specify series, all of the series in the Var will be employed. You may optionally specify the component series by listing the series after an “@” and, if you are using Cholesky weighting for the decomposition, you may change the ordering by listing the order of the series after a second “@”.
By default, EViews computes the decomposition of only the stochastic component into all components using the ordering in the Var. You may instead elect to include the baseline in the decomposition.
Options
m (default) | Display multiple graphs, with the impact of each component on a dependent variable shown in a separate graphs. |
g | Display combined graphs, with decomposition of each variable with respect to all included components shown in one graph. |
imp=arg (default=“chol”) | Type of factorization for the decomposition: unit impulses, ignoring correlations among the residuals (“imp=unit”), non-orthogonal, ignoring correlations among the residuals (“imp=nonort”), Cholesky with d.f. correction (“imp=chol”), Cholesky without d.f. correction (“imp=mlechol”), Generalized (“imp=gen”), structural (“imp=struct”), or user specified (“imp=user”). The structural factorization is based on the estimated structural VAR. To use this option, you must first estimate the structural decomposition; see
Var::svar. For user-specified weights, you must specify the name of the vector/matrix containing the impulses using the “fname=” option. |
baseline | Include the baseline in the decomposition. |
start= date | Start date (within estimation sample) for the decomposition. By default, EViews uses the first date of the estimation sample. |
end = date | End date (within estimation sample) for the decomposition. By default, EViews uses the last date of the estimation sample. |
basename=arg | Optional name fragment used in constructing the names for the series in which to save the decomposition results. If the basename is “base,” the total stochastic or stochastic plus baseline will be saved in the series BASE1, BASE2, etc... (where the numbers in the name correspond to the ordering of the variables in the VAR specification). The components will be saved in the series BASE1_1, BASE1_2, …, BASE2_1, BASE2_2, …., where the numbers after the “_” refer to the ordering of the series in the VAR. Series will be saved only for those variables and components requested above. |
n=arg | Optional name of group object to contain the series created using the "basename=" option. |
prompt | Force the dialog to appear from within a program. |
p | Print the results. |
Examples
var var1.ls 1 4 m1 gdp cpi
var1.hdecomp(10, baseline, m) gdp @ m1 gdp cpi
The first line declares and estimates a VAR with three variables. The second line displays multiple graphs of the historical decomposition of GDP to shocks to the three series in the VAR using the ordering as specified in VAR1. The baseline will be included in the graph.
Cross-references
See
“Vector Autoregression (VAR) Models” for a discussion of historical decomposition in VARs.
Display impulse response functions of var object with an estimated VAR or VEC.
Syntax
var_name.impulse(n, options) [response_series] [@imp impulse_series] [@order ordering_series]
In the syntax above, n is the number of periods over which to compute impulse response functions. When a value for n is not provided, it defaults to 10.
You may optionally filter and sort impulse-response results (for displaying results and outputting results into the workfile) using response_series and impulse_series.
• response_series is a space-delimited list of series names used to filter and sort results based on the response series. It is set to the VAR object’s endog_list by default.
• impulse_series is a space-delimited list of series names used to filter and sort results based on the impulse (shock) series, and is preceded by the keyword “@imp”. It is set to the VAR object’s endog_list by default.
If you are using impulses based on the Cholesky factor, you may specify the Cholesky ordering by listing the order of the series after “@order”. The default behavior is equivalent to setting ordering_series to the VAR object’s endog_list. Note that every variable that appears in the VAR object’s endog_list must be included in ordering_series.
Legacy Syntax
The following syntax has been deprecated:
var_name.impulse(n, options) [response_series] [@ impulse_series [@ ordering_series]]
Mixing the current and legacy syntax is not allowed.
Options
General Options
g | Display combined graphs, with impulse responses of one variable to all shocks shown in one graph. |
m (default) | Display multiple graphs, with impulse response to each shock shown in separate graphs. |
t | Tabulate the impulse responses. |
a | Accumulate the impulse responses. |
imp=arg (default=“chol”) | Type of factorization for the decomposition: unit impulses, ignoring correlations among the residuals (“imp=unit”), non-orthogonal, ignoring correlations among the residuals (“imp=nonort”), Cholesky with d.f. correction (“imp=chol”), Cholesky without d.f. correction (“imp=mlechol”), Generalized (“imp=gen”), structural (“imp=struct”), or user specified (“imp=user”). The structural factorization is based on the estimated structural VAR. To use this option, you must first estimate the structural decomposition; see
Var::svar. For user-specified impulses, you must specify the name of the vector/matrix containing the impulses using the “fname=” option. The option “imp=mlechol” is provided for backward compatibility with EViews 3.x and earlier. |
fname=name | Specify name of vector/matrix containing the impulses. The vector/matrix must have 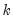 rows and 1 or 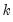 columns, where 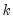 is the number of endogenous variables. |
irtype=arg (default=“ordinary”) | Type of impulse response calculation engine: “ordinary” (classical VAR), “lp” (local projection: sequential), and “lpjoint” (local projection: joint). |
se=arg | Standard error calculations: “se=a” (analytic), “se=mc” (Monte Carlo), “se=boot” (bootstrap). If selecting Monte Carlo or bootstrap, you must specify the number of replications with the “rep=” option. Bootstrap type is set with the “bs=” option. Note the following: (1) Analytic standard errors are currently not available for (a) VECs and (b) structural decompositions identified by long-run restrictions. The “se=a” option will be ignored for these cases. (2) Monte Carlo standard errors are currently not available for (a) VECs and (b) structural decompositions. The “se=mc” option will be ignored for these cases. |
rep=integer | Number of Monte Carlo and bootstrap replications to be used in computing standard errors. Must be used with the “se=mc” and “se=boot” options. |
bs=arg (default = “hp”) | Bootstrap method: “sp” (standard percentile), “hp” (Hall’s percentile), “hs” (Hall’s studentized), “ku” (Killian’s unbiased). Note the following: Hall’s studentized and Kilian’s unbiased bootstraps require a double bootstrap. They can be computed quickly using a fast double bootstrap approximation by supplying an additional “fdb” option. |
dbsrep=integer (default = 499) | Number of double bootstrap replications. Must be used with the “bs=hs” and “bs=ku” options. Note the following: This option is not necessary if supplying the “fdb” option. |
fdb | Approximate double bootstrap routines with fast double bootstrap routines. |
cilevels=arg (default = “0.95”) | Confidence interval coverage as a number between 0 and 1. Note the following: (1) Option is only available when “se=boot”. (2) Multiple confidence levels can be supplied as a space delimited list. |
uselines | Use lines instead of shading for confidence intervals. |
save=name | Save impulse-response estimates in a named matrix. Grouping: Results are grouped by impulse (shock), unless the byrsp keyword is used in which case results are grouped by response. Filtering and sorting: Results are filtered and sorted according to response_series and impulse_series. |
savese=name | Save impulse-response standard errors (or standard deviations) in a named matrix. No output will be generated if the SE/CI method is set to ‘None’. Grouping: Results are grouped by impulse (shock), unless the byrsp keyword is used in which case results are grouped by response. Filtering and sorting: Results are filtered and sorted according to response_series and impulse_series. |
saveci=name | Save impulse-response confidence intervals (or credibility intervals) in a named matrix. No output will be generated if the SE/CI method is set to ‘None’. Grouping: Results are grouped by impulse (shock), unless the byrsp keyword is used in which case results are grouped by response. Filtering and sorting: Results are filtered and sorted according to response_series and impulse_series. |
saverci=name | Save impulse-response estimates and confidence intervals (or credibility intervals) in a named matrix. Estimates are interleaved. No output will be generated if the SE/CI method is set to ‘None’. Grouping: Results are grouped by impulse (shock), unless the byrsp keyword is used in which case results are grouped by response. Filtering and sorting: Results are filtered and sorted according to response_series and impulse_series. |
byrsp | Group results by response instead of by impulse (shock). |
prompt | Force the dialog to appear from within a program. |
p | Print the results. |
BVAR Options
bvartype = arg (default= “bayes”) | Impulse method: Bayesian sampling (“bayes”), classical impulse response analysis using the posterior residual covariance matrix (“classpost”), classical impulse response analysis using the empirical residual covariance matrix (“classemp”). |
If you are using Bayesian sampling, the following Bayesian options are available:
draws=integer (default= 100000) | Number of draws. |
burn=arg (default=0.1) | Proportion of initial draws to discard. |
seed=integer | Random number seed. |
dropunstable | Drop any draws that produce unstable coefficients. |
dgraph | Produce distribution graphs. |
page=arg | Store the individual draws in a new page. |
BTVCVAR Options
dates=arg | Set the impulse date(s). For multiple dates, enter a space-delimited list of values surrounded by quotation marks, e.g., “1980q1 2000q1 2020q1”. |
horizons=arg | Set the elapsed time horizon(s). For multiple horizons, enter a space-delimited list of positive integers surrounded by quotation marks, e.g., “5 9 13”. |
usemean | Use posterior mean as the point estimate. The posterior median is used if usemean is not included in the options list. |
showci | Show credibility intervals (bands). |
Local Projection Options
lpband=arg (default=“marginal”) | Standard error band type: “marginal”, “scheffe”, and “conditional”. Note that marginal error bands do not account for cross-impulse effects, whereas Scheffé and conditional do. |
asym=arg | Asymmetric/nonlinear effects specified as a categorical variable series name or expression. |
Legacy Save (Output to Workfile) Options
The following save options have been deprecated and are only supported for impulse response methods introduced before EViews 13.
Mixing current and legacy save options is not allowed.
matbys=name | (1) Save impulse-response estimates in a named matrix. (2) Save impulse-response standard errors in a named matrix, unless the SE/CI method is set to ‘None’. Grouping: Results are grouped by impulse (shock). Filtering and sorting: Results are neither filtered nor sorted. User’s specifications for response_series and impulse_series are ignored and replaced with the VAR object’s endog_list. |
matbyr=name | (1) Save impulse-response estimates in a named matrix. (2) Save impulse-response standard errors in a named matrix, unless the SE/CI method is set to ‘None’. Grouping: Results are grouped by response. Filtering and sorting: Results are neither filtered nor sorted. User’s specifications for response_series and impulse_series are ignored and replaced with the VAR object’s endog_list. |
smat=name | (1) Save impulse-response estimates in a named matrix. (2) Save impulse-response standard errors in a named matrix, unless the SE/CI method is set to ‘None’. Grouping: Results are grouped by impulse (shock). Filtering and sorting: Results are filtered and sorted according to response_series and impulse_series. |
rmat=name | (1) Save impulse-response estimates in a named matrix. (2) Save impulse-response standard errors in a named matrix, unless the SE/CI method is set to ‘None’. Grouping: Results are grouped by response. Filtering and sorting: Results are filtered and sorted according to response_series and impulse_series. |
cimat=name | (1) Save impulse-response estimates in a named matrix. (2) Save impulse-response confidence intervals in a named matrix, unless the SE/CI method is set to ‘None’. Grouping: Results are grouped by impulse (shock). Filtering and sorting: Results are filtered and sorted according to response_series and impulse_series. |
rcimat=name | (1) Save impulse-response estimates in a named matrix. (2) Save impulse response estimates and confidence intervals in a named matrix, unless the SE/CI method is set to ‘None’. Estimates are interleaved. Grouping: Results are grouped by impulse (shock). Filtering and sorting: Results are filtered and sorted according to response_series and impulse_series. |
Examples
var var1.ls 1 4 m1 gdp cpi
var1.impulse(10,m) gdp
The first line declares and estimates a VAR with three variables. The second line displays multiple graphs of the impulse responses of GDP.
var1.impulse(10,m) gdp @imp m1 @order cpi gdp m1
displays the impulse response of GDP to a one standard deviation shock in M1 using a different ordering.
var.impulse(irtype=lp)
Produces impulse response output for a VAR object called “var” using the sequential local projection impulse response engine.
var.impulse(irtype=lpjoint, asym=@month=6, lpband=scheffe)
Produces impulse response output for a VAR object called “var” using the joint local projection impulse response engine. The standard error band type is set to Scheffé and the asymmetric effect is set to a dummy variable for the month of June. In addition to standard error bands, asymmetric effects are also displayed as two additional curves; one associated with the dummy variable (@month=6) being equal to 0 (false) and the other associated with the dummy variable being equal to 1 (true).
Cross-references
See
“Impulse Response Analysis” for a discussion of impulse responses in VARs.
Multivariate residual normality test.
Syntax
var_name.jbera(options)
You must specify a factorization method using the “factor=” option.
Options
factor=chol | Factorization by the inverse of the Cholesky factor of the residual covariance matrix. |
factor=cor | Factorization by the inverse square root of the residual correlation matrix (Doornik and Hansen, 1994). |
factor=cov | Factorization by the inverse square root of the residual covariance matrix (Urzua, 1997). |
factor=svar | Factorization matrix from structural VAR. You must first estimate the structural factorization to use this option; see
Var::svar. |
name=arg | Save the test statistics in a named matrix object. See below for a description of the statistics contained in the stored matrix. |
prompt | Force the dialog to appear from within a program. |
p | Print the test results. |
The “
name=” option stores the following matrix. Let the VAR have
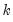
endogenous variables. Then the stored matrix will have dimension
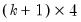
. The first
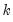
rows contain statistics for each orthogonal component, where the first column contains the third moments, the second column contains the
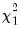
statistics for the third moments, the third column contains the fourth moments, and the fourth column holds the
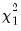
statistics for the fourth moments. The sum of the second and fourth columns are the Jarque-Bera statistics reported in the last output table.
The last row contains statistics for the joint test. The second and fourth column of the
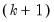
row is simply the sum of all the rows above in the corresponding column and are the
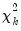
statistics for the joint skewness and kurtosis tests, respectively. These joint skewness and kurtosis statistics add up to the joint Jarque-Bera statistic reported in the output table, except for the “factor=cov” option. When this option is set, the joint Jarque-Bera statistic includes all cross moments (in addition to the pure third and fourth moments). The overall Jarque-Bera statistic for this statistic is stored in the first column of the
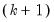
row (which will be a missing value for all other options).
Examples
var var1.ls 1 6 lgdp lm1 lcpi
show var1.jbera(factor=cor,name=jb)
The first line declares and estimates a VAR. The second line carries out the residual multivariate normality test using the inverse square root of the residual correlation matrix as the factorization matrix and stores the results in a matrix named JB.
Cross-references
See
“Vector Autoregression (VAR) Models” for a discussion of the test and other VAR diagnostics.
Display or change the label view of a var object, including the last modified date and display name (if any).
As a procedure, label changes the fields in the var object label.
Syntax
var_name.label
var_name.label(options) [text]
Options
The first version of the command displays the label view of the var object. The second version may be used to modify the label. Specify one of the following options along with optional text. If there is no text provided, the specified field will be cleared.
c | Clears all text fields in the label. |
d | Sets the description field to text. |
s | Sets the source field to text. |
u | Sets the units field to text. |
r | Appends text to the remarks field as an additional line. |
p | Print the label view. |
Examples
The following lines replace the remarks field of VAR1 with “Data from CPS 1988 March File”:
var1.label(r)
var1.label(r) Data from CPS 1988 March File
To append additional remarks to VAR1, and then to print the label view:
var1.label(r) Log of hourly wage
var1.label(p)
To clear and then set the units field, use:
var1.label(u) Millions of bushels
Cross-references
See
“Labeling Objects” for a discussion of labels.
VAR lag order selection criteria.
Syntax
var_name.laglen(m, options)
You must specify the maximum lag order m for which you wish to test.
Options
vname=arg | Save selected lag orders in named vector. See below for a description of the stored vector. |
mname=arg | Save lag order criteria in named matrix. See below for a description of the stored matrix. |
prompt | Force the dialog to appear from within a program. |
p | Print table of lag order criteria. |
The “vname=” option stores a vector with 5 rows containing the selected lags from the following criteria: sequential modified LR test (row 1), final prediction error (row 2), Akaike information criterion (row 3), Schwarz information criterion (row 4), Hannan-Quinn information criterion (row 5).
The “mname=” option stores a
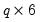
matrix, where
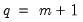
if there are no exogenous variables in the VAR; otherwise
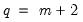
. The first
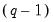
rows contain the information displayed in the table view, following the same order. The saved matrix has an additional row which contains the lag order selected from each column criterion. The first column (corresponding to the log likelihood values) of the last row is always an NA.
Examples
var var1.ls 1 6 lgdp lm1 lcpi
show var1.laglen(12,vname=v1)
The first line declares and estimates a VAR. The second line computes the lag length criteria up to a maximum of 12 lags and stores the selected lag orders in a vector named V1.
Cross-references
See
“Vector Autoregression (VAR) Models” for a discussion of the various criteria and other VAR diagnostics.
Estimate VAR specification.
Syntax
var_name.ls(options) lag_pairs endog_list [@ exog_list] [@restrict restrict_list]
ls estimates an unrestricted VAR using equation-by-equation OLS. You must specify the order of the VAR (using one or more pairs of lag intervals), and then provide a list of series or groups to be used as endogenous variables. You may include exogenous variables such as trends and seasonal dummies in the VAR by including an “@-sign” followed by a list of series or groups. A constant is automatically added to the list of exogenous variables; to estimate a specification without a constant, you should use the option “noconst”.
The
restrict_list is a comma-separated list of text restrictions in the form described below and in greater detail in
“VARs With Linear Constraints”.
Restriction text expressions use the following “@” keywords to refer to individual coefficient matrix elements:
@l#(r, c) | Element (r, c) of the lag # coefficient matrix. |
@e#(r) | Element r of the exogenous variable # coefficient vector. |
@e(X, r) | Element r of the exogenous variable X coefficient vector |
Note that the canonical names (“L#”, “E#”, “E(X)”) that refer to lag matrices and exogenous variable vectors are preceded by “@” to avoid ambiguity.
For example, we may have:
@L1(1,1) = 0
@L2(2,2) = @L1(3,3) / 2
@L2(1,1) + @L4(2,1) = 1
@E(C, 1) = 0
@E(X, 2) = @E(C, 2)
@E1(1) + @E1(2) = 1
In addition, you may use text expressions to refer to parts of lag coefficient matrices and to impose specialized restrictions,
| Restricts all elements of matrix W similar to a pattern matrix. Element ordering matches the vectorization of the matrix, i.e., the elements of the first column, followed by the second column, followed by the third column, etc. |
@diag(W) | Restricts W to be a diagonal matrix, i.e., off-diagonal elements are zero. The diagonal elements are unrestricted. |
@diag(W) = n | Restricts W to be a diagonal matrix with elements on the diagonal restricted to be n. |
@lower(W) | Restricts W to be a lower triangular matrix, i.e., elements above the diagonal are zero. |
@unitlower(W) | Restricts W to be a unit lower triangular matrix, i.e., elements above the diagonal are zero and elements on the diagonal are one. |
@upper(W) | Restricts W to be an upper triangular matrix, i.e., elements below the diagonal are zero. |
@unitupper(W) | Restricts W to be a unit upper triangular matrix, i.e., elements below the diagonal are zero and elements on the diagonal are one. |
@row(W, r) = n | Restricts the elements in row r of W to be n. |
@col(W, c) = n | Restricts the elements in column c of W to be n. |
where
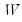
is a reference to a canonical matrix name (
e.g., “L1”, “L3”).
When a “@vec” restriction is included in the restriction list, its own list of values must be enclosed in double quotes, as in
@vec(W) = "1, 2, 3, 4"
Options
General options
noconst | Do not include a constant in exogenous regressors list for VARs. |
prompt | Force the dialog to appear from within a program. |
p | Print basic estimation results. |
Restricted VAR options
noiter | Perform GLS with a single iteration. |
m=integer | Set maximum number of iterations. If iteration and “m=0” then estimation will be by OLS. |
c=scalar | Set convergence criterion. |
showopts / ‑showopts | [Do / do not] display the estimation options in the estimation output. |
Examples
var mvar.ls 1 3 m1 gdp
declares and estimates an unrestricted VAR named MVAR with two endogenous variables (M1 and GDP), a constant and 3 lags (lags 1 through 3).
mvar.ls(noconst) 1 3 ml gdp
estimates the same VAR, but with no constant.
mvar.ls 1 2 dlog(invest) dlog(income) dlog(cons) @restrict @vec(l1) = "na, 0, na, 0, na, na, na, na, na", @vec(l2) = "na, na, na, 0, 0, na, na, na, na"
estimates a VAR with pattern restrictions on elements of the first and second lag matrices.
Cross-references
See also
Var::ec and
Var::bvar for estimation of error correction models and Bayesian VAR estimation.
Creates groups of the coefficient series used to make the BTVCVAR estimation output view.
Creates a series group containing estimates and a series group containing credibility intervals for the coefficients of a BTVCVAR model.
Syntax
var_name.makecoefs c_est_name c_cis_name
Group names can be passed in as arguments. The first argument is the name for the series group containing estimates. The second argument is the name for the series group containing credibility intervals.
Example
var var1.btvcvar 1 1 gdp inflation
var1.makecoefs ests cis
The first line declares and estimates a BTVCVAR for GDP and inflation. The second line produces two coefficient series groups, ests and cis. The est group contains coefficient estimates and the cis group contains credibility intervals for the coefficients.
Create group containing the estimated cointegrating relations from a VEC.
Syntax
var_name.makecoint [group_name]
The series contained in the group are given names of the form “COINTEQ##”, where ## are numbers such that “COINTEQ##” is the next available unused name.
If you provide a name for the group in parentheses after the keyword, EViews will quietly create the named group in the workfile. If you do not provide a name, EViews will open an untitled group window if the command is executed from the command line, otherwise no group will be created.
This proc will return an error message unless you have estimated an error correction model using the var object.
Examples
var vec1.ec(b,2) 1 4 y1 y2 y3
vec1.makecoint gcoint
The first line estimates a VEC with 2 cointegrating relations. The second line creates a group named GCOINT which contains the two estimated cointegrating relations. The two cointegrating relations will be stored as series named COINTEQ01 and COINTEQ02 (if these names have not yet been used in the workfile).
Cross-references
Make a group out of the endogenous series.
Syntax
var_name.makeendog name
Following the keyword makeendog, you should provide a name for the group to hold the endogenous series. If you do not provide a name, EViews will create an untitled group.
Examples
var1.makeendog grp_v1
creates a group named GRP_V1 that contains the endogenous series in VAR1.
Cross-references
Outputs effective sample sizes (ESSs) of the draws of the parameters in a BTVCVAR model.
Generates three matrix objects (one per parameter block) containing ESSs. The ESS for the draws of a parameter is equal to the relative numerical efficiency (RNE) times the posterior sample size. Values near the posterior sample size are desirable. ESSs much smaller than the posterior sample size indicate slow mixing. An NA is returned if sample autocorrelation does not taper off sufficiently quickly (i.e., if sample autocorrelation does not fall below 0.05 in the first 100 lags).
The ESS is the number of IID draws that is needed to achieve the same level of numerical precision as the obtained set of MCMC draws. It measures the extent of efficiency loss for using MCMC instead of vanilla Monte Carlo for sample generation.
The ESS, inefficiency factor, and relative numerical efficiency (RNE) convey the same information and only differ in interpretation.
Syntax
var_name.makeess c_ess_name s_ess_name q_ess_name
Names for the output matrices can be passed in as arguments. ESS matrix names are entered in the order: coefficients (C), observation covariance (S), then process covariance (Q). Untitled matrices are returned if no names are given.
Example
var var1.btvcvar 1 1 gdp inflation
var1.makeess
The first line declares and estimates a BTVCVAR with two variables. Estimation entails posterior simulation, as the posterior distribution is not known analytically. The second line computes and outputs inefficiency factors of the draws obtained.
Cross-references
Outputs inefficiency factors of the draws of the parameters in a BTVCVAR model.
Generates three matrix objects (one per parameter block) containing inefficiency factors. The inefficiency factor of the draws of 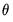 is defined as
is defined as where 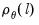 is the sample autocorrelation in the draws of
is the sample autocorrelation in the draws of 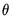 at lag
at lag 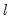 , and
, and 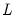 is the lag at which the sample autocorrelation tapers off. Values near one are desirable. Inefficiency factors much greater than one indicate slow mixing. An NA is returned if sample autocorrelation does not taper off sufficiently quickly (i.e., if sample autocorrelation does not fall below 0.05 in the first 100 lags).
is the lag at which the sample autocorrelation tapers off. Values near one are desirable. Inefficiency factors much greater than one indicate slow mixing. An NA is returned if sample autocorrelation does not taper off sufficiently quickly (i.e., if sample autocorrelation does not fall below 0.05 in the first 100 lags). The inefficiency factor can be interpreted as the ratio of the numerical variance of the sample mean computed using MCMC draws and the numerical variance of the sample mean computed using hypothetical IID draws. It measures the extent of efficiency loss for using MCMC instead of vanilla Monte Carlo for sample generation.
The inefficiency factor, relative numerical efficiency (RNE), and effective sample size (ESS) convey the same information and only differ in interpretation.
Syntax
var_name.makeif c_if_name s_if_name q_if_name
Names for the output matrices can be passed in as arguments. Inefficiency factor matrix names are entered in the order: coefficients (C), observation covariance (S), then process covariance (Q). Untitled matrices are returned if no names are given.
Example
var var1.btvcvar 1 1 gdp inflation
var1.makeif
The first line declares and estimates a BTVCVAR with two variables. Estimation requires posterior simulation as the posterior distribution is not known analytically. The second line computes and outputs inefficiency factors of the draws obtained.
Cross-references
Make a model from a var object.
Syntax
var_name.makemodel(name)
If you provide a name for the model in parentheses after the keyword, EViews will create the named model in the workfile. If you do not provide a name, EViews will open an untitled model window if the command is executed from the command line.
Examples
var var3.ls 1 4 m1 gdp tb3
var3.makemodel(varmod)
estimates a VAR and makes a model named VARMOD from the estimated var object. Use the command “show varmod” or “varmod.spec” to open the VARMOD window.
Cross-references
See
“Models” for a discussion of specifying and solving models in EViews.
Save the regime probabilities for switching VAR in series in the workfile.
Syntax
var_name.makergmprobs(options) series_names
where var_name is the name of an switching VAR object. The series to be saved should be listed following the command name and options, with one name per regime for one up to the number of estimated regimes.
Options
type=arg (default=“pred”) | Type of regime probability to compute: one-step ahead predicted (“pred”), filtered (“filt”), smoothed (“smooth”). |
n=arg | (optional) Name of group to contain the saved regime probabilities. |
prompt | Force the dialog to appear from within a program. |
Examples
var var1.switchls(type=markov) y1 y2 y3
var1.makergmprobs r1 r2
saves the one-step ahead regime probabilities for the Markov switching regression estimated in VAR in series R1 and R2 in the workfile
var1.makergmprobs(type=filt) f1
saves the filtered probabilities for regime 1 in F1.
var1.makergmprobs(type=smooth, n=smoothed) s1 s2
saved the smoothed probabilities for both regimes in the series S1 and S2, and creates the group SMOOTHED containing S1 and S2.
Cross-references
See
“Switching VAR” for discussion.
Create residual series.
Creates and saves residuals in the workfile from an estimated VAR.
Syntax
var_name.makeresids(options) [res1 res2 res3]
Follow the VAR name with a period and the makeresids keyword, then provide a list of names to be given to the stored residuals. You should provide as many names as there are equations. If there are fewer names than equations, EViews creates the extra residual series with names RESID01, RESID02, and so on. If you do not provide any names, EViews will also name the residuals RESID01, RESID02, and so on.
Options
struct | Compute structural residuals. |
method = arg | Structural residual method (if “struct” option is provided): unit impulses, ignoring correlations among the residuals (“imp=unit”), non-orthogonal, ignoring correlations among the residuals (“imp=nonort”), Cholesky with d.f. correction (“imp=chol”), Cholesky without d.f. correction (“imp=mlechol”), Generalized (“imp=gen”), structural (“imp=struct”), or user specified (“imp=user”). The structural factorization is based on the estimated structural VAR. To use this option, you must first estimate the structural decomposition; see
Var::svar. For user-specified weights, you must specify the name of the vector/matrix containing the impulses using the “fname=” option. |
n=arg | Create group object to hold the residual series. |
Examples
var macro_var.ls 1 4 y m1 r
macro_var.makeresids resay res_m1 riser
estimates an unrestricted VAR with four lags and endogenous variables Y, M1, and R, and stores the residuals as RES_Y, RES_M1, RES_R.
Cross-references
See
“Views and Procs of a VAR” for a discussion of views and procedures of a VAR.
Outputs relative numerical efficiencies (RNEs) of the draws of the parameters in a BTVCVAR model.
Generates three matrix objects (one per parameter block) containing RNEs. The RNE of the draws of a parameter is the reciprocal of their inefficiency factor. Values near one are desirable. RNEs much smaller than one indicate slow mixing. An NA is returned if sample autocorrelation does not taper off sufficiently quickly (i.e., if sample autocorrelation does not fall below 0.05 in the first 100 lags).
The RNE can be interpreted as the ratio of the numerical variance of the sample mean computed using hypothetical IID draws and the numerical variance of the sample mean computed using MCMC draws. It measures the extent of efficiency loss for using MCMC instead of vanilla Monte Carlo for sample generation.
The RNE, inefficiency factor, and effective sample size (ESS) convey the same information and only differ in interpretation.
Syntax
var_name.makerne c_rne_name s_rne_name q_rne_name
Names for the output matrices can be passed in as arguments. RNE matrix names are entered in the order: coefficients (C), observation covariance (S), then process covariance (Q). Untitled matrices are returned if no names are given.
Example
var var1.btvcvar 1 1 gdp inflation
var1.makerne
The first line declares and estimates a BTVCVAR with two variables. Estimation requires posterior simulation as the posterior distribution is not known analytically. The second line computes and outputs inefficiency factors of the draws obtained.
Cross-references
Create system from a var.
Syntax
var_name.makesystem(options)
You may order the equations by series (default) or by lags.
Options
bylag | Specify system by lags (default is to order by variables). |
n=name | Specify name for the object. |
Examples
var1.makesystem(n=sys1)
creates a system named SYS1 from the var object VAR1
Cross-references
See
“System Estimation” for a discussion of system objects in EViews.
Save the regime transition probabilities and expected durations of switching VAR into the workfile.
Syntax
var_name.maketransprobs(options) [base_name]
var_name.maketransprobs(out=mat, options) [matrix_name]
where VAR_name is the name of a VAR estimated using switching regression.
• In the first form of the command,
base_name will be used to generate series names for the series that will hold the transition probabilities or durations. The series names for regime transition probabilities will be of the form
base_name##, where ## are the indices representing elements of the transition matrix
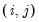
. The series names for expected durations will be of the form
base_name# where # corresponds to the regime index. Thus, in a two-regime model, the base name “TEMP” corresponds to the transition probability series TEMP11, TEMP12, TEMP21, TEMP22, and the expected duration series TEMP1, TEMP2.
If base_name is not provided, EViews will use the default of “TPROB”
• When the option “output=mat” is provided, the matrix_name is the name of the output matrix that will hold the transition probabilities or durations.
If matrix_name are not provided, EViews will default to “TPROB” or the next available name of the form “TPROB##”.
EViews will evaluate the transition probabilities or durations at the date specified by the “obs=” option. If no observation is specified, EViews will use the first date of the estimation sample to evaluate the transition probabilities. Note that if the transition probabilities are time-invariant, setting the observation will have no effect on the contents of the saved results.
Options
type=arg (default=“trans”) | Transition probability results to save: transition probabilities (“trans”), expected durations (“expect”). |
out=arg (default=“series”) | Output format: series (“series”) or matrix (“mat”). If saved as a matrix, only a single transition matrix will be saved using the date specified by “obs=”. |
obs=arg | Date/observation used to evaluate the transition probabilities if saving results as a matrix (“out=mat”). If no observation is specified, EViews will use the first date of the estimation sample to evaluate the transition probabilities. Note that if the transition probabilities are time-invariant, setting the observation will have no effect on the content of the saved results. |
n=arg | (optional) Name of group to contain the saved transition probabilities. |
prompt | Force the dialog to appear from within a program. |
Examples
var var1.switchls(type=markov) y1 y2 y3
var1.maketransprobs(n=transgrp) trans
saves the transition probabilities in the workfile in the series TRANS11, TRANS12, TRANS21, TRANS22 and creates the group TRANSGRP containing the series.
The command
var1.maketransprobs(type=expect) AA
saves the expected durations in the series AA1 and AA2.
var1.maketransprobs(out=mat) BB
saves the transition probabilities in the matrix BB.
Cross-references
See
“Switching VAR” for discussion.
Estimate a mixed frequency VAR specification.
Syntax:
var_name.mfvar(options) var_lag endog_list [@ exog_list] @hf high_freq_list
You must specify the order of the VAR by specifying the maximum lag, and then provide a list of series or groups to be used as endogenous variables.
Exogenous variables such as trends and seasonal dummies in the VAR may then be included by adding “@” followed by a list of series or groups. A constant is automatically added to the list of exogenous variables; to estimate a specification without a constant, you should use the option “noconst”.
For the higher-frequency endogenous variables, you should enter the “@hf” keyword, followed by a list of the variables. The syntax for high frequency variables is pagename\seriesname where pagename is the name of the page containing the series, and seriesname is the name of the series. Note also that series expressions are allowed, e.g. “mypage\log(x)”
Options
General options
noconst | Do not include a constant in exogenous regressors list. |
hfobs = integer | Number of low frequency regressors for each high frequency variable (default is the full number of observations based on the two frequencies, e.g., 3 for monthly data in a quarterly specification). |
bvar | Use Bayesian estimation (default is U-MIDAS). |
last | Use last-period frequency conversion (default is to use the first period). |
lambda = arg | Set the lambda overall tightness hyper-parameter (only applicable with Bayesian estimation where “bvar” is specified). |
uphl = arg | Set the upsilon high-low frequency scale hyper-parameter (only applicable with Bayesian estimation where “bvar” is specified). |
uplh = arg | Set the upsilon low-high frequency scale hyper-parameter (only applicable with Bayesian estimation where “bvar” is specified). |
rhoh = arg | Set the rho high frequency AR(1) hyper-parameter (only applicable with Bayesian estimation where “bvar” is specified). |
rhol = arg | Set the rho low frequency AR(1) hyper-parameter (only applicable with Bayesian estimation where “bvar” is specified). |
initcov= (default =“umidas”) | Initial covariance estimate: U-MIDAS (“umidas”), identity matrix (“identity”) (only applicable with Bayesian estimation where “bvar” is specified). |
kappa = arg | Set the kappa exogenous tightness hyper-parameter (only applicable with Bayesian estimation where “bvar” is specified). |
draws = num (default=100000) | Set the number of MCMC draws (only applicable with Bayesian estimation where “bvar” is specified). |
burn = num (default=0.1) | Set the proportion of MCMC draws to use as a burn-in (only applicable with Bayesian estimation where “bvar” is specified). |
seed = num | Set the seed for the MCMC generator (only applicable with Bayesian estimation where “bvar” is specified). |
prompt | Force the dialog to appear from within a program. |
p | Print basic estimation results. |
Examples
Cross-references
See also
Var::ls and
Var::ec for estimation of ordinary VARs and error correction models.
Push updates to OLE linked objects in open applications.
Syntax
var_name.olepush
Cross-references
See
“Object Linking and Embedding (OLE)” for a discussion of using OLE with EViews.
Display estimation output.
output changes the default object view to display the estimation output (equivalent to using
Var::results).
Syntax
var_name.output
For BTVCVARs, the following syntax can be used to specify the coefficient series to display in the estimation output view:
var_name.output [@var var_list] [@lag lag_list] [@exog exog_list]
where var_list is a list of (endogenous) variables, lag_list is a list of lags, and exog_list is a list of exogenous variables. Each list is specified using a key-value pair, where the key (@var, @lag, or @exog) indicates the list type, and the value (var_list, lag_list, or exog_list) is a space-delimited list of items to select.
Leave a list unspecified (i.e., omit the associated key-value pair) to select every item in the list in the order in which they appear at the time of estimation. To specify an empty list, include the key but leave the value blank.
Options
p | Print estimation output for estimation object |
Examples
The output keyword may be used to change the default view of an estimation object. Entering the command:
var1.output
displays the estimation output for VAR1.
var var2.btvcvar 1 2 4 4 gdp infl @ c unemp
var2.output @var gdp @lag 1 4
shows the coefficient series corresponding to GDP(-1), GDP(-4), C, and UNEMP for the BTVCVAR VAR2. Note that C and UNEMP are included (selected) because exog_list is unspecified. To hide coefficients on exogenous variables, use the following instead:
var2.output @var gdp @lag 1 4 @exog
Cross-references
Puts posterior draws of a BTVCVAR model in a new page.
Creates a copy of a posterior sample and pastes it into a new page. A series represents draws for a particular parameter. EViews will prompt you to run the posterior sampler if draws are not available.
Syntax
var_name.postdraws page_name
Examples
myvar.postdraws mydraws
creates a new page called mydraws containing a copy of the posterior sample for the BTVCVAR var object MYVAR.
Posterior residual covariance matrix.
Syntax
var_name.postresidcov(options)
Options
p | Print the posterior residual covariance matrix. |
Examples
var1.postresidcov
displays the posterior residual covariance matrix of VAR1.
Multivariate residual autocorrelation Portmanteau tests.
Syntax
var_name.qstats(h, options)
You must specify the highest order of lag h to test for serial correlation. h must be larger than the VAR lag order.
Options
name=arg | Save Q-statistics in the named matrix object. The matrix has two columns: the first column contains the unmodified Q-statistic; the second column contains the modified Q-statistics. |
prompt | Force the dialog to appear from within a program. |
p | Print the Portmanteau test results. |
Examples
var var1.ls 1 6 lgdp lm1 lcpi
show var1.qstats(l0, name=q)
The first line declares and estimates a VAR. The second line displays the portmanteau tests for lags up to 10, and stores the Q-statistics in a matrix named Q.
Cross-references
See
“Diagnostic Views” for a discussion of the Portmanteau tests and other VAR diagnostics.
See
Var::arlm for a related multivariate residual serial correlation LM test.
Display text of specification for var objects.
Syntax
var_name.representation(options)
Options
p | Print the representation text. |
Examples
var1.representations
displays the specifications of the estimation object VAR1.
Cross-references
Residual correlation matrix.
Displays the correlations of the residuals from each equation in the var object.
Note that for Bayesian VARs, this command will display the empirical residual correlation—the correlation of the residuals calculated from the posterior means of the coefficients.
Syntax
var_name.residcor(options)
Options
p | Print the correlation matrix. |
Examples
var1.residcor
displays the residual correlation matrix of VAR1.
Cross-references
Residual covariance matrix.
Displays the covariances of the residuals from each equation in the var object.
Note that for Bayesian VARs, this command will display the empirical residual covariance—the covariance of the residuals calculated from the posterior means of the coefficients.
Syntax
var_name.residcov(options)
Options
p | Print the covariance matrix. |
Examples
var1.residcov
displays the residual covariance matrix of VAR1.
Cross-references
Display residuals.
resids displays multiple graphs of the residuals. Each graph will contain the residuals for an equation in the VAR.
Syntax
var_name.resids(options)
Options
struct | Compute structural residuals. |
method = arg | Structural residual method (if “struct” option is provided): unit impulses, ignoring correlations among the residuals (“imp=unit”), non-orthogonal, ignoring correlations among the residuals (“imp=nonort”), Cholesky with d.f. correction (“imp=chol”), Cholesky without d.f. correction (“imp=mlechol”), Generalized (“imp=gen”), structural (“imp=struct”), or user specified (“imp=user”). The structural factorization is based on the estimated structural VAR. To use this option, you must first estimate the structural decomposition; see
Var::svar. For user-specified weights, you must specify the name of the vector/matrix containing the impulses using the “fname=” option. |
p | Print the table/graph. |
Examples
var var1.ls 1 3 m1 c
var1.resids
calculates a VAR with three lags, two endogenous variables and a constant term, and then displays a graph of the residuals.
Cross-references
Displays the results view of an estimated VAR.
Syntax
var_name.results(options)
Options
Examples
var mvar.ls 1 4 8 8 m1 gdp tb3 @ @trend(70.4)
mvar.results(p)
prints the estimation results from the estimated VAR.
Display regime probabilities for a switching VAR.
Syntax
var_name.rgmprobs(options) [indices]
where var_name is the name of a switching VAR object. The elements to display are given by the optional indices corresponding to the regimes (e.g., “1 2 3” or “2 3”). If indices is not provided, results for all of the regimes will be displayed.
Options
type=arg (default=“pred”) | Type of regime probability to compute: one-step ahead predicted (“pred”), filtered (“filt”), smoothed (“smooth”). |
view=arg (default=“graph”) | Display format: multiple graphs (“graph”), single graph “graph1”, sheet (“sheet”), summary (“summary”). |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Examples
var var1.switchls(type=markov) y1 y2 y3
var1.rgmprobs
displays graphs containing the one-step ahead regime probabilities for the Markov switching VAR estimated in VAR1.
var1.rgmprobs(type=filt) 2
displays the filtered probabilities for regime 2.
var1.rgmprobs(type=smooth, view=graph1)
displays the smoothed probabilities for both regimes in a single graph.
Cross-references
See
“Switching VAR” for discussion.
Set the object attribute.
Syntax
var_name.setattr(attr) attr_value
Sets the attribute attr to attr_value. Note that quoting the arguments may be required. Once added to an object, the attribute may be extracted using the @attr data member.
Examples
a.setattr(revised) never
String s = a.@attr("revised")
sets the “revised” attribute in the object A to the string “never”, and extracts the attribute into the string object S.
Cross-references
Estimate factorization matrix for structural innovations.
Syntax
var_name.svar(options)
The var object must previously have been estimated in unrestricted form.
You must specify the identifying restrictions either in text form by the
append proc or by a pattern matrix option. See
“Specifying SVAR Restrictions in EViews” for details on specifying restrictions.
Options
You may specify any of the following options:
a=mat | Name of the pattern matrix for factorization matrix A. |
b=mat | Name of the pattern matrix for factorization matrix B. |
s=mat | Name of the pattern matrix for short-run impulse response matrix S. |
f=mat | Name of the pattern matrix for long-run impulse response matrix F. |
f0=arg (default=0.1) | Specify the starting values for estimation free parameters: a scalar value, or ‘s’ for user-specified values in the C coefficient object, or ‘u’ for values randomly drawn from the uniform distribution on [0,1], or ‘n’ for values randomly drawn from the standard normal distribution. The default is a scalar value of 0.1. |
maxiter=num, m=num | Maximum number of optimization iterations. The default is taken from the global option settings. |
conv=num, c=num | The convergence criterion (lower bound on optimization step size). The default is taken from the global option settings. |
trace=num, t=num (default=0) | Summarize the ongoing optimization every num iterations. Summary information is displayed in an unnamed text object. The default is a trace period of 0, which disables tracing. |
fsign | Do not perform sign normalization. See “
“Sign Restrictions”” for a description of sign normalization. |
nostop | Suppress “Near Singular Matrix” and other error messages during estimation. |
preset=num, p=num | Apply a restriction preset, as described in the SVAR Options Identifying Restrictions dialog. num may be 1 through 6, corresponding to the first six preset options. |
prompt | Force the dialog to appear from within a program. |
Examples
var var1.ls 1 4 m1 gdp cpi
matrix(3,3) pata
pata.fill 1, na, na, 0, 1, na, 0, 0, 1
matrix(3,3) patb
pata.fill na, 0, 0, 0, na, 0, 0, 0, na
var1.svar(a=pata,b=patb)
The first line declares and estimates a VAR with three variables. We then create the factorization pattern matrices and perform the estimation.
var var1.ls 1 8 dy u @
var1.append(svar) @f(2,1)=0
freeze(out1) var1.svar
The first line declares and estimates a VAR with two variables without a constant. The next two lines specify a long-run restriction and store the estimation output in a table object named OUT1.
Cross-references
See
“Structural (Identified) VARs” for a discussion of structural VARs.
Estimate a switching VAR specification.
Syntax:
var_name.switchvar(options) lag_pairs endog_list [@ exog_list] [ @prv list_of_probability_regressors ]
You must specify the order of the VAR (using one or more pairs of lag intervals), and then provide a list of series or groups to be used as endogenous variables. You may include exogenous variables such as trends and seasonal dummies in the VAR by including an “@-sign” followed by a list of series or groups. A constant is automatically added to the list of exogenous variables; to estimate a specification without a constant, you should use the option “noconst”.
Options
General options
msm | Switching mean specification (default is switching intercept). |
exognv | Exogenous variables are non-regime specific (default is for exogenous variables to vary). |
endogvary | Lagged endogenous variables are regime specific (default is for the endogenous variables to be non-varying). |
noconst | Do not include a constant in exogenous regressors list. |
fprobmat=arg | Name of fixed transition probability matrix allows for fixing specific elements of the time-invariant transition matrix. Leave NAs in elements of the matrix to estimate. The 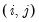 element of the matrix corresponds to 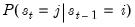 . |
initprob=arg (default=“ergodic”) | Method for determining initial Markov regime probabilities: ergodic solution (“ergodic”), estimated parameter (“est”), equal probabilities (“uniform”), user-specified probabilities (“user”). If “initprob=user” is specified, you will need to specify the “userinit=” option. |
userinit=arg | Name of vector containing user-specified initial Markov probabilities. The vector should have rows equal to the number of states; we expand this to the size of the initial lag state vector where necessary for AR specifications. For use in specifications containing both the “type=markov” and “initprob=user” options. |
startnum=arg (default=0 or 25) | Number of random starting values tried. The default is 0 for user-supplied coefficients (option “s”) and 25 in all other cases. |
startiter=arg (default=10) | Number of iterations taken after each random start before comparing objective to determine final starting value. |
searchnum=arg (default=0) | Number of post-estimation perturbed starting values tried. |
searchsds=arg (default=1) | Number of standard deviations to use in perturbed starts (if “searchnum=”) is specified. |
seed=positive_integer from 0 to 2,147,483,647 | Seed the random number generator. If not specified, EViews will seed random number generator with a single integer draw from the default global random number generator. |
rnd= arg (default=“kn” or method previously set using
rndseed). | Type of random number generator: improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4”) L’Ecuyer’s (1999) combined multiple recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). |
In addition to the specification options, there are options for estimation and covariance calculation.
Additional Options
optmethod = arg | Optimization method: “bfgs” (BFGS); “newton” (Newton-Raphson), “opg” or “bhhh” (OPG or BHHH), “legacy” (EViews legacy). BFGS is the default method. |
optstep = arg | Step method: “marquardt” (Marquardt); “dogleg” (Dogleg); “linesearch” (Line search). Marquardt is the default method. |
m=integer | Set maximum number of iterations. |
c=scalar | Set convergence criterion. The criterion is based upon the maximum of the percentage changes in the scaled coefficients. The criterion will be set to the nearest value between 1e-24 and 0.2. |
cov=arg | Covariance method: “ordinary” (default method based on inverse of the estimated information matrix), “huber” or “white” (Huber-White sandwich method). |
covinfo = arg | Information matrix method: “opg” (OPG); “hessian” (observed Hessian). (Applicable when non-legacy “optmethod=”.) |
nodf | Do not degree-of-freedom correct the coefficient covariance estimate. |
coef=arg | Specify the name of the coefficient vector (if specified by list); the default behavior is to use the “C” coefficient vector. |
s | Use the current coefficient values in “C” as starting values (see also
param). |
s=number | Specify a number between zero and one to determine starting values as a fraction of EViews default values (out of range values are set to “s=1”). |
showopts / ‑showopts | [Do / do not] display the starting coefficient values and estimation options in the estimation output. |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Examples
var01.switchvar(type=markov) 1 3 m1 gdp
declares and estimates a MSI(2)-VAR(3) with two endogenous variables (M1 and GDP) and a switching constant.
var01.switchvar(type=markov, msm) 1 3 m1 gdp
estimates the MSM(2)-VAR(3) variant of the same specification..
var01.switchvar(type=markov, msm, endogvary, seed=1551063419) 1 3 m1 gdp
estimates a MSMA(2)-VAR(3) specification.
Cross-references
See
“Switching VAR” for details.
See also
Var::ls and
Var::ec for estimation of ordinary VARs and error correction models.
Perform exogeneity (Granger causality) tests on a VAR.
Syntax
var_name.testexog(options)
Options
name=arg | Save the Wald test statistics in named matrix object. See below for a description of the statistics stored in the matrix. |
p | Print output from the test. |
The
name= option stores the results in a
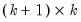
matrix, where
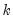
is the number of endogenous variables in the VAR. In the first
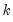
rows, the
i-th row,
j-th column contains the Wald statistic for the joint significance of lags of the
i-th endogenous variable in the
j-th equation (note that the entries in the main diagonal are not reported in the table view). The degrees of freedom of the Wald statistics is the number of lags included in the VAR.
In the last row, the
j-th column contains the Wald statistic for the joint significance of all lagged endogenous variables (excluding lags of the dependent variable) in the
j-th equation. The degrees of freedom of the Wald statistics in the last row is
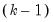
times the number of lags included in the VAR.
Examples
var var1.ls 1 6 lgdp lm1 lcpi
freeze(tab1) var1.testexog(name=exog)
The first line declares and estimates a VAR. The second line stores the exclusion test results in a named table TAB1, and stores the Wald statistics in a matrix named EXOG.
Cross-references
See
“Diagnostic Views” for a discussion of other VAR diagnostics.
Perform lag exclusion (Wald) tests on a VAR.
Syntax
var_name.testlags(options)
Options
name=arg | Save the Wald test statistics in named matrix object. See below for a description of the statistics contained in the stored matrix. |
p | Print the result of the test. |
The “
name=” option stores results in an
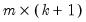
matrix, where
is the number of lagged terms and
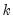
is the number of endogenous variables in the VAR. In the first
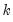
columns, the
i-th row,
j-th column entry is the Wald statistic for the joint significance of all
i-th lagged endogenous variables in the
j-th equation. These Wald statistics have a
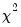
distribution with
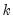
degrees of freedom under the exclusion null.
In the last column, the
i-th row contains the system Wald statistic for testing the joint significance of all
i-th lagged endogenous variables in the VAR system. The system Wald statistics has a chi-square distribution with
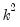
degrees of freedom under the exclusion null.
Examples
var var1.ls 1 6 lgdp lm1 lcpi
freeze(tab1) var1.testlags(name=lags)
The first line declares and estimates a VAR. The second line stores the lag exclusion test results in a table named TAB1, and stores the Wald statistics in a matrix named LAGS.
Cross-references
See
“Diagnostic Views” for a discussion other VAR diagnostics.
Display regime transition probabilities and expected durations for a switching VAR.
Syntax
var_name.transprobs(options)
where equation_name is the name of an equation estimated using switching regression.
Options
type=arg (default=“summary”) | Transition probability results to display: summary (“default”), transition probabilities (“trans”), expected durations (“expect”). The default summary displays the transition matrix and expected regime durations for constant transition probability models, and descriptive statistics for the transition and expected durations for varying probability models. |
view=arg (default=“graph”) | Display method: graph (“graph”), spreadsheet (“sheet”), table (“table”). Applicable when displaying the transition probabilities or expected durations (“type=trans” or “type=expect”). The spreadsheet form represents shows the transition probabilities or regime expected durations in columns and observations in rows. The table form displays the transition probabilities or expected durations in a table (in a single matrix for a time-constant model, and individual matrices for a time-varying model). |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Examples
var var1.switchls(type=markov) y1 y2 y3
var1.transprobs
displays the default summary of the transition probabilities estimated in VAR1.
The command
var1.transprobs(type=trans)
displays the transition probabilities in a graph, while
var1.transprobs(type=trans, view=sheet)
displays the transition probabilities in a spreadsheet, with each row column representing one of the probabilities and each row representing an observation.
var1.transprobs(type=trans, view=table)
displays the transition probabilities in a table.
var1.transprobs(type=expect, view=sheet)
displays the expected durations in spreadsheet form.
Cross-references
See
“Switching VAR” for discussion.
Declare a var (Vector Autoregression) object.
Syntax
var var_name
var var_name.ls(options) lag_pairs endog_list [@ exog_list]
var var_name.ec(trend, n) lag_pairs endog_list [@ exog_list]
var var_name.bvar(trend, n) lag_pairs endog_list [@ exog_list]
var var_name.btvcvar(options) lag_pairs endog_list [@ exog_list]
var var_name.mfvar(options) var_lag endog_list [@ exog_list] @hf high_freq_list
var var_name.switchreg(options) lag_pairs endog_list [@ exog_list] [ @prv list_of_probability_regressors ]
Declare the var as a name, or a name followed by an estimation method and specification.
Examples
var mvar.ls 1 4 8 8 m1 gdp tb3 @ @trend
declares and estimates an unrestricted VAR named MVAR with three endogenous variables (M1, GDP, TB3), five lagged terms (lags 1 through 4, and 8), a constant, and a linear trend.
var jvar.ec(c,2) 1 4 m1 gdp tb3
declares and estimates an error correction model named JVAR with three endogenous variables (M1, GDP, TB3), four lagged terms (lags 1 through 4), two cointegrating relations. The “c” option assumes a linear trend in data but only a constant in the cointegrating relations.
Cross-references
See
“Vector Autoregression (VAR) Models” for a discussion of vector autoregressions and EC models.
See
Var::ls for specification of a standard VAR.
See
Var::ec for the error correction specification of a VAR.
See
Var::bvar for the specification of a Bayesian VAR.
See
Var::btvcvar for the specification of a Bayesian Time-varying Coefficient VAR.
See
Var::mfvar for the specification of a mixed-frequency VAR.
See
Var::switchvar for the specification of a switching VAR.
Variance decomposition in VARs.
Syntax
var_name.vdecomp(n, options) [response_series] [@comp component_series] [@order ordering_series]
In the syntax above, n is the number of periods over which to compute variance decompositions. When a value for n is not provided, it defaults to 10.
You may optionally filter and sort variance decomposition results (for displaying results and outputting results into the workfile) using response_series and component_series.
• response_series is a space-delimited list of series names used to filter and sort results based on the response (decomposition) series. It is set to the VAR object’s endog_list by default.
• component_series is a space-delimited list of series names used to filter and sort results based on the component series, and is preceded by the keyword “@comp”. It is set to the VAR object’s endog_list by default.
If using Cholesky factorization, you may specify the Cholesky ordering by listing the order of the series after “@order”. The default behavior is equivalent to setting ordering_series to the VAR object’s endog_list. Note that every variable that appears in the VAR object’s endog_list must be included in ordering_series.
Legacy Syntax
The following syntax has been deprecated:
var_name.vdecomp(n, options) [response_series] [@ @ ordering_series]
var_name.decomp(n, options) [response_series] [@ @ ordering_series]
While you may use the older forms of the command, mixing the current and legacy syntax is not allowed.
Options
General Options
g | Display combined graphs, with the decompositions for each variable shown in a graph. |
m | Display multiple graphs, with each response-component pair shown in a separate graph. |
t (default) | Show numerical results in table. |
imp=arg (default=“chol”) | Type of factorization for the decomposition: “chol” (Cholesky with d.f. correction), “mlechol” (Cholesky without d.f. correction), “struct” (structural). The structural factorization is based on the estimated structural VAR. To use this option, you must first estimate the structural decomposition; see
Var::svar. The option “imp=mlechol” is provided for backward compatibility with EViews 3.x and earlier. |
se=mcarlo | Monte Carlo standard errors. You must specify the number of replications with the “rep=” option. Currently available only when you have specified the Cholesky factorization (using the “imp=chol” option). |
rep=integer | Number of Monte Carlo replications to be used in computing the standard errors. Must be used with the “se=mcarlo” option. |
cilevels=arg (default = “0.95”) | Confidence interval coverage: space limited list of numbers between 0 and 1. |
uselines | Use lines instead of shading for confidence intervals. |
save=name | Save variance decomposition estimates in a named matrix. Grouping: Results are grouped by component, unless the byrsp keyword is used in which case results are grouped by response (decomposition). Filtering and sorting: Results are filtered and sorted according to response_series and component_series. |
savese=name | Save variance decomposition standard errors in a named matrix. No output will be generated if the SE/CI method is set to ‘None’. Grouping: Results are grouped by component, unless the byrsp keyword is used in which case results are grouped by response (decomposition). Filtering and sorting: Results are filtered and sorted according to response_series and component_series. |
saveci=name | Save variance decomposition confidence intervals in a named matrix. No output will be generated if the SE/CI method is set to ‘None’. Grouping: Results are grouped by component, unless the byrsp keyword is used in which case results are grouped by response (decomposition). Filtering and sorting: Results are filtered and sorted according to response_series and component_series. |
saverci=name | Save variance decomposition estimates and confidence intervals in a named matrix. Estimates are interleaved. No output will be generated if the SE/CI method is set to ‘None’. Grouping: Results are grouped by component, unless the byrsp keyword is used in which case results are grouped by response (decomposition). Filtering and sorting: Results are filtered and sorted according to response_series and component_series. |
savefse=name | Save forecast standard errors in a named matrix. Filtering and sorting: Results are filtered and sorted according to response_series. |
byrsp | Group results by response (decomposition) instead of by component. |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Legacy Save (Output to Workfile) Options
The following save options have been deprecated and are only supported for variance decomposition methods introduced before EViews 13.
Mixing current and legacy save options is not allowed.
matbys=name | (1) Save variance decomposition estimates in a named matrix. (2) Save forecast standard errors in a named matrix. (3) Save variance decomposition standard errors in a named matrix, unless the SE/CI method is set to ‘None’. Grouping: Results are grouped by component. Filtering and sorting: Results are neither filtered nor sorted. User’s specifications for response_series and component_series are ignored and replaced with the VAR object’s endog_list. |
matbyr=name | (1) Save variance decomposition estimates in a named matrix. (2) Save forecast standard errors in a named matrix. (3) Save variance decomposition standard errors in a named matrix, unless the SE/CI method is set to ‘None’. Grouping: Results are grouped by response (decomposition). Filtering and sorting: Results are neither filtered nor sorted. User’s specifications for response_series and component_series are ignored and replaced with the VAR object’s endog_list. |
Examples
var var1.ls 1 4 m1 gdp cpi
var1.vdecomp(10,t) gdp
The first line declares and estimates a VAR with three variables and lags from 1 to 4. The second line tabulates the variance decompositions of GDP up to 10 periods using the ordering as specified in VAR1.
var1.vdecomp(10,t) gdp @order cpi gdp m1
performs the same variance decomposition as above using a different Cholesky ordering.
Cross-references
See
“Variance Decomposition” for additional details.
Performs White’s test for heteroskedasticity of residuals.
Carries out White’s multivariate test for heteroskedasticity of the residuals of the specified Var object. By default, the test is computed without the cross-product terms (using only the terms involving the original variables and squares of the original variables). You may elect to compute the original form of the White test that includes the cross-products.
Syntax
var_name.white(options)
Options
c | Include all possible nonredundant cross-product terms in the test regression. |
name=arg | Save test statistics in named matrix object. See below for a description of the statistics stored in the matrix. |
p | Print the test results. |
The “
name=” option stores the results in a
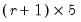
matrix, where
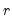
is the number of unique residual cross-product terms. For a VAR with
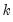
endogenous variables,
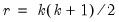
. The first
rows contain statistics for each individual test equation, where the first column is the regression R-squared, the second column is the
F-statistic, the third column is the
p-value of
F-statistic, the 4th column is the
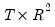
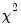
statistic, and the fifth column is the
p-value of the
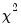
statistic.
The numerator and denominator degrees of freedom of the
F-statistic are stored in the third and fourth columns, respectively, of the
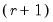
-
st row, while the

degrees of freedom is stored in the fifth column of the
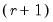
-
st row.
In the
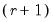
-
st row and first column contains the joint (system) LM chi-square statistic and the second column contains the degrees of freedom of this
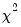
statistic.
Examples
var1.white
carries out the White test of heteroskedasticity.
Cross-references
See
“White's Heteroskedasticity Test” for a discussion of White’s test. For the multivariate version of this test, see
“White Heteroskedasticity Test”.
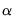 (where applicable).
(where applicable).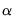 (where applicable).
(where applicable).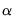 (where applicable).
(where applicable).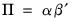 (where applicable).
(where applicable).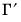 (where applicable).
(where applicable).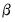 (where applicable).
(where applicable).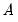 ,
, 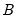 ,
, 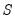 , and
, and 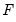 .
. 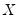 can be substituted with any of the canonical matrices
can be substituted with any of the canonical matrices 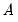 ,
, 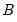 ,
, 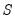 , and
, and 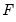 . The canonical names should not be preceded by “@” in this context since there is no potential workfile object ambiguity in the function argument(s).
. The canonical names should not be preceded by “@” in this context since there is no potential workfile object ambiguity in the function argument(s). ,
,  ,
, 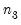 , ...
, ...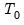 . A prior sample is not used if T0 is set to 0. To use a prior sample, T0 must be set to an integer larger than the number of coefficients per equation in a standard VAR version of the model.
. A prior sample is not used if T0 is set to 0. To use a prior sample, T0 must be set to an integer larger than the number of coefficients per equation in a standard VAR version of the model. .
. .
.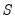 .
.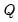 .
.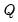 .
.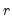 indicates that every
indicates that every 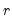 -th draw after the burn-in period is stored.
-th draw after the burn-in period is stored.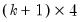 matrix, where
matrix, where 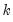 is the number of endogenous variables in the VAR. The first column contains the eigenvalues, the second column contains the maximum eigenvalue statistics, the third column contains the trace statistics, and the fourth column contains the log likelihood values. The i-th row of columns 2 and 3 are the test statistics for rank
is the number of endogenous variables in the VAR. The first column contains the eigenvalues, the second column contains the maximum eigenvalue statistics, the third column contains the trace statistics, and the fourth column contains the log likelihood values. The i-th row of columns 2 and 3 are the test statistics for rank 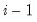 . The last row is filled with NAs, except the last column which contains the log likelihood value of the unrestricted (full rank) model.
. The last row is filled with NAs, except the last column which contains the log likelihood value of the unrestricted (full rank) model. 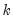 rows and 1 or
rows and 1 or 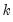 columns, where
columns, where 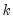 is the number of endogenous variables.
is the number of endogenous variables.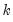 endogenous variables. Then the stored matrix will have dimension
endogenous variables. Then the stored matrix will have dimension 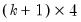 . The first
. The first 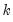 rows contain statistics for each orthogonal component, where the first column contains the third moments, the second column contains the
rows contain statistics for each orthogonal component, where the first column contains the third moments, the second column contains the 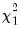 statistics for the third moments, the third column contains the fourth moments, and the fourth column holds the
statistics for the third moments, the third column contains the fourth moments, and the fourth column holds the 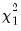 statistics for the fourth moments. The sum of the second and fourth columns are the Jarque-Bera statistics reported in the last output table.
statistics for the fourth moments. The sum of the second and fourth columns are the Jarque-Bera statistics reported in the last output table.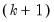 row is simply the sum of all the rows above in the corresponding column and are the
row is simply the sum of all the rows above in the corresponding column and are the 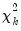 statistics for the joint skewness and kurtosis tests, respectively. These joint skewness and kurtosis statistics add up to the joint Jarque-Bera statistic reported in the output table, except for the “factor=cov” option. When this option is set, the joint Jarque-Bera statistic includes all cross moments (in addition to the pure third and fourth moments). The overall Jarque-Bera statistic for this statistic is stored in the first column of the
statistics for the joint skewness and kurtosis tests, respectively. These joint skewness and kurtosis statistics add up to the joint Jarque-Bera statistic reported in the output table, except for the “factor=cov” option. When this option is set, the joint Jarque-Bera statistic includes all cross moments (in addition to the pure third and fourth moments). The overall Jarque-Bera statistic for this statistic is stored in the first column of the 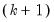 row (which will be a missing value for all other options).
row (which will be a missing value for all other options).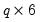 matrix, where
matrix, where 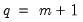 if there are no exogenous variables in the VAR; otherwise
if there are no exogenous variables in the VAR; otherwise 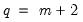 . The first
. The first 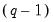 rows contain the information displayed in the table view, following the same order. The saved matrix has an additional row which contains the lag order selected from each column criterion. The first column (corresponding to the log likelihood values) of the last row is always an NA.
rows contain the information displayed in the table view, following the same order. The saved matrix has an additional row which contains the lag order selected from each column criterion. The first column (corresponding to the log likelihood values) of the last row is always an NA.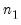 ,
, 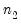 ,
, 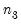 , ...
, ...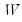 is a reference to a canonical matrix name (e.g., “L1”, “L3”).
is a reference to a canonical matrix name (e.g., “L1”, “L3”).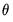 is defined as
is defined as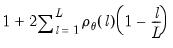
 is the sample autocorrelation in the draws of
is the sample autocorrelation in the draws of  at lag
at lag  , and
, and 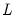 is the lag at which the sample autocorrelation tapers off. Values near one are desirable. Inefficiency factors much greater than one indicate slow mixing. An NA is returned if sample autocorrelation does not taper off sufficiently quickly (i.e., if sample autocorrelation does not fall below 0.05 in the first 100 lags).
is the lag at which the sample autocorrelation tapers off. Values near one are desirable. Inefficiency factors much greater than one indicate slow mixing. An NA is returned if sample autocorrelation does not taper off sufficiently quickly (i.e., if sample autocorrelation does not fall below 0.05 in the first 100 lags).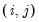 . The series names for expected durations will be of the form base_name# where # corresponds to the regime index. Thus, in a two-regime model, the base name “TEMP” corresponds to the transition probability series TEMP11, TEMP12, TEMP21, TEMP22, and the expected duration series TEMP1, TEMP2.
. The series names for expected durations will be of the form base_name# where # corresponds to the regime index. Thus, in a two-regime model, the base name “TEMP” corresponds to the transition probability series TEMP11, TEMP12, TEMP21, TEMP22, and the expected duration series TEMP1, TEMP2. 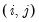 element of the matrix corresponds to
element of the matrix corresponds to  .
.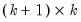 matrix, where
matrix, where 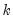 is the number of endogenous variables in the VAR. In the first
is the number of endogenous variables in the VAR. In the first 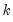 rows, the i-th row, j-th column contains the Wald statistic for the joint significance of lags of the i-th endogenous variable in the j-th equation (note that the entries in the main diagonal are not reported in the table view). The degrees of freedom of the Wald statistics is the number of lags included in the VAR.
rows, the i-th row, j-th column contains the Wald statistic for the joint significance of lags of the i-th endogenous variable in the j-th equation (note that the entries in the main diagonal are not reported in the table view). The degrees of freedom of the Wald statistics is the number of lags included in the VAR.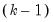 times the number of lags included in the VAR.
times the number of lags included in the VAR.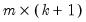 matrix, where
matrix, where  is the number of lagged terms and
is the number of lagged terms and  is the number of endogenous variables in the VAR. In the first
is the number of endogenous variables in the VAR. In the first  columns, the i-th row, j-th column entry is the Wald statistic for the joint significance of all i-th lagged endogenous variables in the j-th equation. These Wald statistics have a
columns, the i-th row, j-th column entry is the Wald statistic for the joint significance of all i-th lagged endogenous variables in the j-th equation. These Wald statistics have a 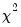 distribution with
distribution with 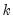 degrees of freedom under the exclusion null.
degrees of freedom under the exclusion null.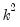 degrees of freedom under the exclusion null.
degrees of freedom under the exclusion null.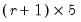 matrix, where
matrix, where 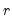 is the number of unique residual cross-product terms. For a VAR with
is the number of unique residual cross-product terms. For a VAR with 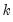 endogenous variables,
endogenous variables, 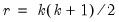 . The first
. The first 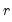 rows contain statistics for each individual test equation, where the first column is the regression R-squared, the second column is the F-statistic, the third column is the p-value of F-statistic, the 4th column is the
rows contain statistics for each individual test equation, where the first column is the regression R-squared, the second column is the F-statistic, the third column is the p-value of F-statistic, the 4th column is the 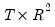
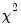 statistic, and the fifth column is the p-value of the
statistic, and the fifth column is the p-value of the 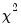 statistic.
statistic. 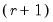 -st row, while the
-st row, while the  degrees of freedom is stored in the fifth column of the
degrees of freedom is stored in the fifth column of the 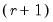 -st row.
-st row. 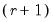 -st row and first column contains the joint (system) LM chi-square statistic and the second column contains the degrees of freedom of this
-st row and first column contains the joint (system) LM chi-square statistic and the second column contains the degrees of freedom of this 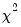 statistic.
statistic.