Copying Data Between Objects
In addition to the basic assignment statements described in the previous section, EViews provides you with a large set of tools for copying data to and from matrix objects.
At times, you may wish to move data between different types of matrix objects. For example, you may wish to take the data from a vector and put it in a matrix. EViews has a number of built-in rules which make these conversions automatically.
At other times, you may wish to move data between a matrix object and an EViews series or group object. There are a separate set of tools which allow you to convert data across a variety of object types.
Copying Data From Matrix Objects
Data may be moved between different types of matrix objects using assignment statements. If possible, EViews will resize the target object so that it contains the same information as the object on the right side of the equation.
The basic rules governing expressions of the form “Y=X” may be summarized as follows:
• The object type of the target Y cannot change.
• The target object Y will, if possible, be resized to match the object X; otherwise, EViews will issue an error. Thus, assigning a vector to a matrix will resize the matrix, but assigning a matrix to a vector will generate an error if the matrix has more than one column.
• The data in X will be copied to Y.
Specific exceptions to the rules given above are:
• If X is a scalar, Y will keep its original size and will be filled with the value of X.
• If X and Y are both vector or rowvector objects, Y will be changed to the same type as X.
Here are some simple examples illustrating the rules for matrix assignment:
vector(3) x
x(1) = 1
x(2) = 2
x(3) = 3
vector y = x
matrix z = x
Y is now a 3 element vector because it has the same dimension and values as
X. EViews automatically resizes the
Z Matrix to conform to the dimensions of
X so that
Z is now a
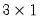
matrix containing the contents of
X:
Z(1,1)=1,
Z(2,1)=2,
Z(3,1)=3.
Here are some further examples where automatic resizing is allowed:
vector(7) y = 2
scalar value = 4
matrix(10,10) w = value
w = y
matrix(2,3) x = 1
rowvector(10) t = 100
x = t
W is declared as a
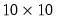
matrix of 4’s, but it is then reset to be a
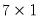
matrix of 2’s.
X is a
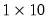
matrix of 100’s.
Lastly, consider the commands:
vector(7) y = 2
rowvector(12) z = 3
coef(20) beta
y = z
z = beta
Y will be a rowvector of length 3, containing the original contents of Z, and Z will be a column vector of length 20 containing the contents of BETA.
There are some cases where EViews will be unable to perform the specified assignment because the resize operation is ill defined. For example, suppose that
X is a
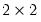
matrix. Then the assignment statement:
vector(7) y = x
will result in an error. EViews cannot change Y from a vector to a matrix and there is no way to assign directly the 4 elements of the matrix X to the vector Y. Other examples of invalid assignment statements involve assigning matrix objects to scalars or sym objects to vector objects.
It may be possible, however, to use the
@vec,
@vech,
@unvec, and
@unvech functions to reshape matrices and vectors into forms that permit assignment.
Extracting Part of a Matrix Objects
The best way to extract data from a matrix object is to use matrix object member functions.
Basic Submatrix Extraction
The relevant functions for all matrix objects are:
• obj.@col(arg) – returns matrix object containing column(s) of obj associated with arg
• obj.@row(arg) – returns matrix object containing row(s) of obj associated with arg
• obj.@sub(arg1, arg2) – returns matrix object containing row(s) and col(s) of obj associated with arg1 and arg2, respectively
• obj.@dropcol(arg) – returns matrix object containing column(s) of obj not associated with arg
• obj.@droprow(arg) – returns matrix object containing row(s) of obj not associated with arg
• obj.@dropboth(arg1, arg2) – returns matrix object containing row(s) and col(s) of obj not associated with arg1 and arg2, respectively
For symmetric matrices, we also have the functions
• obj.@ssub(arg) – returns sym object containing row(s) and col(s) of obj associated with arg, respectively
• obj.@dropboth(arg) – returns sym object containing row(s) and col(s) of obj not associated with arg, respectively
where
• obj is the name of a matrix object in the workfile
• arg, arg1, arg2 are integers, scalar objects, vectors, strings, or svectors
For cases where args are numeric (integers, scalars, vectors), the arg values act as row or column indices. Focusing on column functions, for example,
vector v1 = x.@col(3)
matrix m1 = x.@col(cid)
where X is a matrix and CID is a vector of column indices, and the two lines return the vector V1 and matrix M1 containing the 3rd column of X, and the columns of X referenced in CID, respectively. Note that the elements of CID must be integers from 1 to the number of columns of X.
For cases where args are strings (string literal, string object, svector), the arg values are examined to find matches in the corresponding row or column labels . For example, the commands
vector v2 = x.@col("apple")
matrix m2 = x.@col(scid)
where SCID is a svector of strings, produce the vector V2 and matrix M2 containing the 3rd column of X, and the columns of X with labels that match the elements of SCID, respectively. Note that all of the elements of SCID must be strings that match the column names previously assigned to X.
You may mix the types of arg1 and arg2 in data member functions that take two arguments so that, for example,
matrix m3 = x.@sub(3, "apple")
returns M3 containing the element of X in row 3 and column with label “apple”.
Similarly, the commands
matrix v1d = x.@dropcol(3)
matrix m1d = x.@dropcol(cid)
matrix v2d = x.@dropcol("apple")
matrix m2d = x.@dropcol(scid)
matrix m3d = x.@dropboth(5, "apple")
return the matrix objects
• V1D, the matrix X with column 3 dropped
• M1D, the matrix X with columns referenced by CID dropped
• V2D, the matrix X with the column with label “apple” dropped
• M2D, the matrix X with the columns with labels in SCID dropped
• M3D, the matrix with the row 5 dropped and the column labeled “apple” dropped
The special symmetric matrix versions of these functions return syms:
sym sym1 = symorig.@ssub(cid)
sym sym2 = symorig.@dropcol(3)
sym sym3 = symorig.@dropcol(cid)
return the sym objects
• SYM1, the columns (and corresponding rows) of SYMORIG referenced by CID
• SYM2, the contents of SYMORIG after dropping column and row 3
• V2D, the contents of SYMORIG after dropping columns and rows referenced by CID
Submatrix Extraction using Utility Functions
Combining matrix utility functions (
“Initialize Using Creation Functions”) with the matrix extraction data members offers flexible methods for obtaining data from matrices.
Consider, for example, the extraction of multiple columns from the matrix X using the @col data member function:
vector xid = @fill(1, 3, 5, 9)
matrix xsub = x.@col(xid)
extracts columns {1, 3, 5, 9} from the matrix X.
Since the args in the member data extraction functions may themselves be expressions, we may combine the two lines into a single expression:
matrix xsub1 = x.@col(@fill(1, 3, 5, 9))
Similarly, extracting or dropping the 7 through 9th columns of X may be done using
matrix xsub2 = x.@col(@range(7, 9))
matrix xsub3 = x.@dropcol(@range(7, 9))
We can perform the same compound extractions in 2-dimensions, as in
matrix xsub4 = x.@sub(@range(3, 6), @sfill("apple", "orange"))
matrix xsub5 = x.@dropboth(4, @sfill("apple", "orange"))
which create XSUB4 containing rows 3 to 6 and columns with labels matching “apple” and “orange” of X, and XSUB5 containing X after dropping row 4 and the columns with matching labels.
Assigning to Part of a Matrix Objects
Data from a matrix may be assigned to part of another matrix object using the commands
colplace,
rowplace, and
matplace. Consider the commands:
matrix(100,5) m1 = 0
matrix(100,2) m2 = 1
vector(100) v1 = 3
rowvector(100) v2 = 4
matplace(m1,m2,1,3)
colplace(m1,v1,3)
rowplace(m1,v2,80)
The matplace command places M2 in M1 beginning at row 1 and column 3. V1 is placed in column 3 of M1, while V2 is placed in row 80 of M1.
You may combine
matplace with
@fill and the
@row,
@col,
@droprow, or
@dropcol data members to perform complex subsetting and filling
matplace(z, x.@row(@fill(1, 3, 4)), 1, 1)
puts rows 1, 3, and 4 of the matrix X into the upper-left hand corner of Z. Note that Z must be large enough to hold the X subset.
Copying Data Between Matrices and Series/Groups
The previous sections described techniques for copying data between matrix objects such as vectors, matrices and scalars. In this section, we describe techniques for copying data between matrix objects and workfile-based EViews objects such as series and groups.
Keep in mind that there are two primary differences between the ordinary series or group objects and the matrix objects. First, operations involving series and groups use information about the current workfile sample, while matrix objects do not. Second, there are important differences in the handling of missing values (NAs) between the two types of objects.
Direct Assignment
The easiest method to copy data from series or group objects to a matrix object is to use direct assignment. Place the destination matrix object on the left side of an equal sign, and place the series or group to be converted on the right.
If you use a series object on the right-hand side and a vector on the left, EViews will only use observations from the current sample to make the vector. If you place a group object on the right and a matrix on the left, EViews will create a rectangular matrix out of the group using observations from the current sample.
While direct assignment is straightforward and convenient, there are two principal limitations to the approach. First, EViews uses only the observations in the current sample when copying the data. Second, observations containing missing data (NAs) for a series, or for any series in the group, are dropped. Thus, if the current sample contains 20 observations, but the series or group contains missing data, the dimension of the output vector or matrix will be less than 20. (Below, we describe methods which allow you to override the current sample and to retain missing values.)
Examples:
smpl 1963m03 1993m06
fetch hsf gmpyq
group mygrp hsf gmpyq
vector xvec = gmpyq
matrix xmat = mygrp
These statements create the vector XVEC and the two column matrix XMAT containing the non-missing series and group data from 1963M03 to 1993M06. Note that if GMPYQ has a missing value in 1970M01, and HSF contains a missing value in 1980M01, both observations for both series will be excluded from XMAT.
When performing matrix assignment, you may refer to an element of a series, just as you would refer to an element of a vector, by placing an index value in parentheses after the name. An index value i refers to the i-th element of the series from the beginning of the workfile range, not the current sample. For example, if the range of the current annual workfile is 1961 to 1980, the expression GNP(6) refers to the 1966 value of GNP. These series element expressions may be used in assigning specific series values to matrix elements, or to assign matrix values to a specific series element. For example:
matrix(5,10) x
series yser = nrnd
x(1,1) = yser(4)
yser(5) = x(2,3)
yser(6) = 4000.2
assigns the fourth value of the series YSER to X(1,1), and assigns to the fifth and sixth values of YSER, the X(2,3) value and the scalar value “4000.2”, respectively.
While matrix assignments allow you to refer to elements of series as though they were elements of vectors, you cannot generally use series in place of vectors. Most vector and matrix operations will error if you use a series in place of a vector. For example, you cannot perform a rowplace command using a series name.
Furthermore, note that when you are not performing matrix assignment, a series name followed by a number in parentheses will indicate that the lag/lead operator be applied to the entire series. Thus, when used in generating series or in an equation, system, or model specification, GNP(6) refers to the sixth lead of the GNP series. To refer to specific elements of the GNP series in these settings, you should use the @elem function.
Copy using @convert
The
@convert function takes a series or group object and, optionally, a sample object, and returns a vector or rectangular matrix. If no sample is provided,
@convert will use the workfile sample. The sample determines which series elements are included in the matrix. Example:
smpl 61 90
group groupx inv gdp m1
vector v = @convert(gdp)
matrix x = @convert(groupx)
X is a
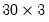
matrix with the first column containing data from
INV, the second column from
GDP, and the third column from
M1.
As with direct assignment,
@convert excludes observations for which the series or any of the series in the group contain missing data. If, in the example above,
INV contains missing observations in 1970 and 1980,
V would be a 29 element vector while
X would be a
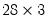
matrix. This will cause errors in subsequent operations that require
V and
X to have a common row dimension.
There are two primary advantages of using @convert over direct assignment. First, since @convert is a function, it may be used in the middle of a matrix expression. Second, an optional second argument allows you to specify a sample to be used in conversion. For example:
sample s1.set 1950 1990
matrix x = @convert(grp, s1)
sym y = @inverse(@inner(@convert(grp, s1)))
performs the conversion using the sample defined in S1.
Copy using Commands
EViews also provides three useful commands that perform explicit conversions between series and matrices with control over both the sample and the handling of NAs.
stom (
Series
TO Matrix) takes a series or group object and copies its data to a vector or matrix using either the current workfile sample, or the optionally specified sample. As with direct assignment, the
stom command excludes observations for which the series or any of the series in the group contain missing data.
Example:
sample smpl_cnvrt.set 1950 1995
smpl 1961 1990
group group1 gnp gdp money
vector(46) vec1
matrix(3,30) mat1
stom(gdp, vec1, smpl_cnvrt)
stom(group1, mat1)
While the operation of stom is similar to @convert, stom is a command and cannot be included in a matrix expression. Furthermore, unlike @convert, the destination matrix or vector must already exist and have the proper dimension.
stomna (
Series
TO Matrix with
NAs) works identically to
stom, but does not exclude observations for which there are missing values. The elements of the series for the relevant sample will map directly into the target vector or matrix. Thus,
smpl 1951 2000
vector(50) gvector
stom(gdp, gvector)
will always create a 50 element vector GVECTOR that contains the values of GDP from 1951 to 2000, including observations with NAs.
mtos (
Matrix
TO Series) takes a matrix or vector and copies its data into an existing series or group, using the current workfile sample or a sample that you provide.
Example:
mtos(mat1, group1)
mtos(vec1, resid)
mtos(mat2, group1, smpl1)
As with stom the destination dimension given by the sample must match that of the source vector or matrix.
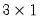 matrix containing the contents of X: Z(1,1)=1, Z(2,1)=2, Z(3,1)=3.
matrix containing the contents of X: Z(1,1)=1, Z(2,1)=2, Z(3,1)=3. 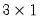 matrix containing the contents of X: Z(1,1)=1, Z(2,1)=2, Z(3,1)=3.
matrix containing the contents of X: Z(1,1)=1, Z(2,1)=2, Z(3,1)=3. 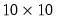 matrix of 4’s, but it is then reset to be a
matrix of 4’s, but it is then reset to be a 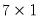 matrix of 2’s.
matrix of 2’s. 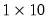 matrix of 100’s.
matrix of 100’s.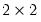 matrix. Then the assignment statement:
matrix. Then the assignment statement: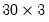 matrix with the first column containing data from
matrix with the first column containing data from 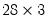 matrix. This will cause errors in subsequent operations that require
matrix. This will cause errors in subsequent operations that require