Estimation by generalized method of moments (GMM).
Syntax
gmm(options) y x1 [x2 x3...] @ z1 [z2 z3...]
gmm(options) specification @ z1 [z2 z3...]
Follow the name of the dependent variable by a list of regressors, followed by the “@” symbol, and a list of instrumental variables which are orthogonal to the residuals. Alternatively, you can specify an expression using coefficients, an “@” symbol, and a list of instrumental variables. There must be at least as many instrumental variables as there are coefficients to be estimated.
In panel settings, you may specify dynamic instruments corresponding to predetermined variables. To specify a dynamic instrument, you should tag the instrument using “@DYN”, as in “@DYN(X)”. By default, EViews will use a set of period-specific instruments corresponding to lags from -2 to “-infinity”. You may also specify a restricted lag range using arguments in the “@DYN” tag. For example, to use lags from-5 to “-infinity” you may enter “@DYN(X, -5)”; to specify lags from -2 to -6, use “@DYN(X, -2, -6)” or “@DYN(X, -6, -2)”.
Note that dynamic instrument specifications may easily generate excessively large numbers of instruments.
Options
Non-Panel GMM Options
Basic GMM Options
nocinst | Do not include automatically a constant as an instrument. |
method=keyword | Set the weight updating method. keyword should be one of the following: “nstep” (N-Step Iterative, or Sequential N-Step Iterative, default), “converge” (Iterate to Convergence or Sequential Iterate to Convergence), “simul” (Simultaneous Iterate to Convergence), “oneplusone” (One-Step Weights Plus One Iteration), or “cue” (Continuously Updating”. |
gmmiter=integer | Number of weight iterations. Only applicable if the “method=nstep” option is set. |
w=arg | Weight series or expression. |
wtype=arg (default=“istdev”) | Weight specification type: inverse standard deviation (“istdev”), inverse variance (“ivar”), standard deviation (“stdev”), variance (“var”). |
wscale=arg | Weight scaling: EViews default (“eviews”), average (“avg”), none (“none”). The default setting depends upon the weight type: “eviews” if “wtype=istdev”, “avg” for all others. |
s | Use the current coefficient values in estimator coefficient vector as starting values for equations specified by list with AR or MA terms (see also
param). |
s=number | Determine starting values for equations specified by list with AR or MA terms. Specify a number between zero and one representing the fraction of TSLS estimates computed without AR or MA terms to be used. Note that out of range values are set to “s=1”. Specifying “s=0” initializes coefficients to zero. By default EViews uses “s=1”. Does not apply to coefficients for AR and MA terms which are instead set to EViews determined default values. |
m=integer | Maximum number of iterations. |
c=number | Set convergence criterion. The criterion is based upon the maximum of the percentage changes in the scaled coefficients. The criterion will be set to the nearest value between 1e-24 and 0.2. |
l=number | Set maximum number of iterations on the first-stage iteration to get the one-step weighting matrix. |
numericderiv / ‑numericderiv | [Do / do not] use numeric derivatives only. If omitted, EViews will follow the global default. |
fastderiv / ‑fastderiv | [Do / do not] use fast derivative computation. If omitted, EViews will follow the global default. |
showopts / ‑showopts | [Do / do not] display the starting coefficient values and estimation options in the estimation output. |
coef=arg | Specify the name of the coefficient vector (if specified by list); the default behavior is to use the “C” coefficient vector. |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Estimation Weighting Matrix Options
instwgt=keyword | Set the estimation weighting matrix type. Keyword should be one of the following: “tsls” (two-stage least squares), “white” (White diagonal matrix), “hac” (Newey-West HAC, default) or “user” (user defined). |
instwgtmat=name | Set the name of the user-defined estimation weighting matrix. Only applicable if the “instwgt=user” option is set. |
instlag=arg (default=1) | Whitening Lag specification: integer (user-specified lag value), “a” (automatic selection). |
instinfosel=arg (default=“aic”) | Information criterion for automatic whitening lag selection: “aic” (Akaike), “sic” (Schwarz), “hqc” (Hannan-Quinn) (if “instlag=a”). |
instmaxlag= integer | Maximum lag-length for automatic selection (optional) (if “instlag=a”). The default is an observation-based maximum of 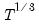 . |
instkern=arg (default=“bart”) | Kernel shape: “none” (no kernel), “bart” (Bartlett, default), “bohman” (Bohman), “daniell” (Daniell), “parzen” (Parzen), “parzriesz” (Parzen-Riesz), “parzgeo” (Parzen-Geometric), “parzcauchy” (Parzen-Cauchy), “quadspec” (Quadratic Spectral), “trunc” (Truncated), “thamm” (Tukey-Hamming), “thann” (Tukey-Hanning), “tparz” (Tukey-Parzen). |
instbw=arg (default=“fixednw”) | Kernel Bandwidth: “fixednw” (Newey-West fixed), “andrews” (Andrews automatic), “neweywest” (Newey-West automatic), number (User-specified bandwidth). |
instnwlag=integer | Newey-West lag-selection parameter for use in nonparametric bandwidth selection (if “instbw=neweywest”). |
instbwint | Use integer portion of bandwidth. |
Covariance Options
cov=keyword | Covariance weighting matrix type (optional): “updated” (estimation updated), “tsls” (two-stage least squares), “white” (White diagonal matrix), “hac” (Newey-West HAC), “wind” (Windmeijer) or “user” (user defined). The default is to use the estimation weighting matrix. |
nodf | Do not perform degree of freedom corrections in computing coefficient covariance matrix. The default is to use degree of freedom corrections. |
covwgtmat=name | Set the name of the user-definied covariance weighting matrix. Only applicable if the “covwgt=user” option is set. |
covlag=arg (default=1) | Whitening lag specification: integer (user-specified lag value), “a” (automatic selection). |
covinfosel=arg (default=”aic”) | Information criterion for automatic selection: “aic” (Akaike), “sic” (Schwarz), “hqc” (Hannan-Quinn) (if “lag=a”). |
covmaxlag=integer | Maximum lag-length for automatic selection (optional) (if “lag=a”). The default is an observation-based maximum of 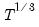 . |
covkern=arg (default=“bart”) | Kernel shape: “none” (no kernel), “bart” (Bartlett, default), “bohman” (Bohman), “daniell” (Daniel), “parzen” (Parzen), “parzriesz” (Parzen-Riesz), “parzgeo” (Parzen-Geometric), “parzcauchy” (Parzen-Cauchy), “quadspec” (Quadratic Spectral), “trunc” (Truncated), “thamm” (Tukey-Hamming), “thann” (Tukey-Hanning), “tparz” (Tukey-Parzen). |
covbw=arg (default=“fixednw”) | Kernel Bandwidth: “fixednw” (Newey-West fixed), “andrews” (Andrews automatic), “neweywest” (Newey-West automatic), number (User-specified bandwidth). |
covnwlag=integer | Newey-West lag-selection parameter for use in nonparametric kernel bandwidth selection (if “covbw=neweywest”). |
covbwint | Use integer portion of bandwidth. |
Panel GMM Options
cx=arg | Cross-section effects method: (default) none, fixed effects estimation (“cx=f”), first-difference estimation (“cx=fd”), orthogonal deviation estimation (“cx=od”) |
per=arg | Period effects method: (default) none, fixed effects estimation (“per=f”). |
levelper | Period dummies always specified in levels (even if one of the transformation methods is used, “cx=fd” or “cx=od”). |
wgt=arg | GLS weighting: (default) none, cross-section system weights (“wgt=cxsur”), period system weights (“wgt=persur”), cross-section diagonal weighs (“wgt=cxdiag”), period diagonal weights (“wgt=perdiag”). |
gmm=arg | GMM weighting: 2SLS (“gmm=2sls”), White period system covariances (Arellano-Bond 2-step/n-step) (“gmm=perwhite”), White cross-section system (“gmm=cxwhite”), White diagonal (“gmm=stackedwhite”), Period system (“gmm=persur”), Cross-section system (“gmm=cxsur”), Period heteroskedastic (“cov=perdiag”), Cross-section heteroskedastic (“gmm=cxdiag”). By default, uses the identity matrix unless estimated with first difference transformation (“cx=fd”), in which case, uses (Arellano-Bond 1-step) difference weighting matrix. In this latter case, you should specify 2SLS weights (“gmm=2sls”) for Anderson-Hsiao estimation. |
cov=arg | Coefficient covariance method: (default) ordinary, White cross-section system robust (“cov=cxwhite”), White period system robust (“cov=perwhite”), White heteroskedasticity robust (“cov=stackedwhite”), Cross-section system robust/PCSE (“cov=cxsur”), Period system robust/PCSE (“cov=persur”), Cross-section heteroskedasticity robust/PCSE (“cov=cxdiag”), Period heteroskedasticity robust (“cov=perdiag”). |
keepwgts | Keep full set of GLS/GMM weights used in estimation with object, if applicable (by default, only weights which take up little memory are saved). |
coef=arg | Specify the name of the coefficient vector (if specified by list); the default behavior is to use the “C” coefficient vector. |
iter=arg (default=“onec”) | Iteration control for GLS and GMM weighting specifications: perform one weight iteration, then iterate coefficients to convergence (“iter=onec”), iterate weights and coefficients simultaneously to convergence (“iter=sim”), iterate weights and coefficients sequentially to convergence (“iter=seq”), perform one weight iteration, then one coefficient step (“iter=oneb”). |
s | Use the current coefficient values in estimator coefficient vector as starting values for equations specified by list with AR or MA terms (see also
param). |
s=number | Determine starting values for equations specified by list with AR terms. Specify a number between zero and one representing the fraction of TSLS estimates computed without AR terms to be used. Note that out of range values are set to “s=1”. Specifying “s=0” initializes coefficients to zero. By default EViews uses “s=1”. Does not apply to coefficients for AR terms which are instead set to EViews determined default values. |
m=integer | Maximum number of iterations. |
c=number | Set convergence criterion. The criterion is based upon the maximum of the percentage changes in the scaled coefficients. The criterion will be set to the nearest value between 1e-24 and 0.2. |
l=number | Set maximum number of iterations on the first-stage iteration to get the one-step weighting matrix. |
unbalsur | Compute SUR factorization in unbalanced data using the subset of available observations for a cluster. |
numericderiv / ‑numericderiv | [Do / do not] use numeric derivatives only. If omitted, EViews will follow the global default. |
fastderiv / ‑fastderiv | [Do / do not] use fast derivative computation. If omitted, EViews will follow the global default. |
showopts / ‑showopts | [Do / do not] display the starting coefficient values and estimation options in the estimation output. |
p | Print results. |
Note that some options are only available for a subset of specifications.
Examples
In a non-panel workfile, we may estimate equations using the standard GMM options. The specification:
gmm(instwgt=white,gmmiter=2,nodf) cons c y y(-1) w @ c p(-1) k(-1) x(-1) tm wg g t
estimates the Klein equation for consumption using GMM with a White diagonal weighting matrix (two steps and no degree of freedom correction). The command:
gmm(method=cue,instwgt=hac,instlag=1,instkern=thann, instbw=andrews,nodf) i c y y(-1) k(-1) @ c p(-1) k(-1) x(-1) tm wg g t
estimates the Klein equation for investment using a Newey-West HAC weighting matrix, with pre-whitening with 1 lag, a Tukey-Hanning kernel and the Andrews automatic bandwidth routine. The estimation is performed using continuously updating weight iterations.
When working with a workfile that has a panel structure, you may use the panel equation estimation options. The command
gmm(cx=fd, per=f) dj dj(-1) @ @dyn(dj)
estimates an Arellano-Bond “1-step” estimator with differencing of the dependent variable DJ, period fixed effects, and dynamic instruments constructed using DJ with observation specific lags from period
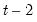
to 1.
To perform the “2-step” version of this estimator, you may use:
gmm(cx=fd, per=f, gmm=perwhite, iter=oneb) dj dj(-1) @ @dyn(dj)
where the combination of the options “gmm=perwhite” and (the default) “iter=oneb” instructs EViews to estimate the model with the difference weights, to use the estimates to form period covariance GMM weights, and then re-estimate the model.
You may iterate the GMM weights to convergence using:
gmm(cx=fd, per=f, gmm=perwhite, iter=seq) dj dj(-1) @ @dyn(dj)
Alternately:
gmm(cx=od, gmm=perwhite, iter=oneb) dj dj(-1) x y @ @dyn(dj,-2,-6) x(-1) y(-1)
estimates an Arellano-Bond “2-step” equation using orthogonal deviations of the dependent variable, dynamic instruments constructed from DJ from period
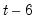
to
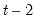
, and ordinary instruments X(-1) and Y(-1).
Cross-references
See
“Generalized Method of Moments” and
“Panel Estimation” for discussion of the various GMM estimation techniques.
See
Equation::gmm for the equivalent equation object command.
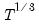 .
.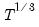 .
.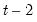 to 1.
to 1.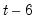 to
to 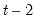 , and ordinary instruments X(-1) and Y(-1).
, and ordinary instruments X(-1) and Y(-1).