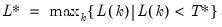Maximum likelihood estimation of the factor model.
Syntax
factor_name.ml(options) x1 [x2 x3...] [@partial z1 z2 z3...]
factor_name.ml(options) matrix_name [[obs] [conditioning]] [@ name1 name2 name3...]
The first method computes the observed dispersion matrix from a set of series or group objects. Simply append a period and the ml keyword to the name of your object, followed by the names of your series and groups, You may optionally use the keyword @partial and append a list of conditioning series.
In the second method you will provide the name of the observed dispersion matrix, and optionally, the number of observations and the rank of the set of conditioning variables. If the latter is not provided, it will be set to 1 (representing the constant in the standard centered variance calculations). You may also provide names for the columns of the correlation matrix by entering the @-sign followed by a list of valid series names.
Options
Estimation Options
rescale | Rescale the uniqueness and loadings estimates so that they match the observed variances. |
maxit=integer | Maximum number of iterations. |
conv=scalar | Set convergence criterion. The criterion is based upon the maximum of the percentage changes in the scaled estimates. The criterion will be set to the nearest value between 1e-24 and 0.2. |
showopts / ‑showopts | [Do / do not] display the starting coefficient values and estimation options in the rotation output. |
prompt | Force the dialog to appear from within a program. |
p | Print basic estimation results. |
Number of Factors Options
n=arg or fsmethod=arg (default=“map”) | Number of factors: “kaiser” (Kaiser-Guttman greater than mean), “mineigen” (Minimum eigenvalue criterion; specified using “eiglimit”), “varfrac” (fraction of variance accounted for; specified using “varlimit”), “map” (Velicer’s Minimum Average Partial method), “bstick” (comparison with broken stick distribution), “parallel” (parallel analysis: number of replications specified using “pnreps”; “pquant” indicates the quantile method value if employed), “scree” (standard error scree method), “bn” (Bai and Ng (2002)), “ah” (Ahn and Horenstein (2013)), integer (user-specified integer value). |
eiglimit=number (default=1) | Limit value for retaining factors using the eigenvalue comparison (where “n=mineigen”). |
varlimit=number (default=0.5) | Fraction of total variance explained limit for retaining factors using the variance limit criterion (where “n=varlimit”). |
porig | Use the unreduced matrix for parallel analysis (the default is to use the reduced matrix). For parallel analysis only (“n=parallel”). |
preps= integer (default=100) | Number of parallel analysis repetitions. For parallel analysis only (“n=parallel”). |
pquant=number | Quantile value for parallel analysis comparison (if not specified, the mean value will be employed). For parallel analysis only (“n=parallel”). |
pseed=positive integer | Seed the random number generator for parallel analysis. If not specified, EViews will seed the random number generator with a single integer draw from the default global random number generator. For parallel analysis only (“n=parallel”). |
prnd= arg (default=“kn” or method previously set using
rndseed) | Type of random number generator for the simulation: improved Knuth generator (“kn”), improved Mersenne Twister (“mt”), Knuth’s (1997) lagged Fibonacci generator used in EViews 4 (“kn4”) L’Ecuyer’s (1999) combined multiple recursive generator (“le”), Matsumoto and Nishimura’s (1998) Mersenne Twister used in EViews 4 (“mt4”). For parallel analysis only (“n=parallel”). |
mfmethod=arg (default=“user”) | Maximum number of components used by selection methods: “schwert” (Schwert’s rule, default), “ah” (Ahn and Horenstein’s (2013) suggestion), “rootsize” ( 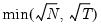 ), “size” ( 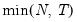 ) ), “user” (user specified value), where 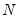 is the number of series and 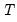 is the number of observations. (1) For use with all components retention methods apart from user-specified (“fsmethod=user”). (2) If setting “mfmethod=user”, you may specify the maximum number of components using “rmax=”. (3) Schwert’s rule sets the maximum number of components using the rule: let for 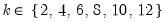 and let and let 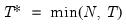 ; then the default maximum lag is given by ; then the default maximum lag is given by |
rmax=arg (default=all) | User-specified maximum number of factors to retain (for use when “mfmethod=user”). |
fsic=arg (default=avg) | Factor selection criterion (when “fsmethod=bn”): “icp1” (ICP1), “icp2” (ICP2), “icp3” (ICP3), “pcp1” (PCP1), “pcp2” (PCP1), “pcp3” (ICP3), “avg” (average of all criteria ICP1 through PCP3). Factor selection criterion (when “fsmethod=ah”): “er” (eigenvalue ratio), “gr” (growth ratio), “avg” (average of eigenvalue ratio and growth ratio). Factor selection criterion (when “fsmethod=simple”): “min” (minimum of: minimum eigenvalue, cumulative eigenvalue proportion, and maximum number of factors), “max” (maximum of: minimum eigenvalue, cumulative eigenvalue proportion, and maximum number of factors), “avg” (average the optimal number of factors as specified by the min and max rule, then round to the nearest integer). |
demeantime | Demeans observations across time prior to component selection procedures, when “n=bn” or “n=ah”. |
sdizetime | Standardizes observations across time prior to component selection procedures, when “n=bn” or “n=ah”. |
demeancross | Demeans observations across cross-sections prior to component selection procedures, when “n=bn” or “n=ah”. |
sdizecross | Standardizes observations across cross-sections prior to component selection procedures, when “n=bn” or “n=ah”. |
Initial Communalities Options
priors=arg | Method for obtaining initial communalities: “smc” (squared multiple correlations), “max” (maximum absolute correlation”), “pace” (noniterative partitioned covariance estimation), “frac” (fraction of the diagonals of the original matrix; specified using “priorfrac=”), “random” (random fractions of the original diagonals), “user” (user-specified vector; specified using “priorunique”). |
priorfrac=number | User-specified common fraction (between 0 and 1) to be used when “priors=frac”. |
priorunique=arg | Vector of initial uniqueness estimates to be used when “priors=user”. By default, the values will be taken from the corresponding elements of the coefficient vector C. |
Covariance Options
cov=arg (default=“cov”) | Covariance calculation method: ordinary (Pearson product moment) covariance (“cov”), ordinary correlation (“corr”), Spearman rank covariance (“rcov”), Spearman rank correlation (“rcorr”), Kendall’s tau-b (“taub”), Kendall’s tau-a (“taua”), uncentered ordinary covariance (“ucov”), uncentered ordinary correlation (“ucorr”). User-specified covariances are indicated by specifying a sym matrix object in place of a list of series or groups in the command. |
wgt=name (optional) | Name of series containing weights. |
wgtmethod=arg (default = “sstdev”) | Weighting method (when weights are specified using “weight=”): frequency (“freq”), inverse of variances (“var”), inverse of standard deviation (“stdev”), scaled inverse of variances (“svar”), scaled inverse of standard deviations (“sstdev”). Only applicable for ordinary (Pearson) calculations. Weights specified by “wgt=” are frequency weights for rank correlation and Kendall’s tau calculations. |
pairwise | Compute using pairwise deletion of observations with missing cases (pairwise samples). |
df | Compute covariances with a degree-of-freedom correction for the mean (for centered specifications), and any partial conditioning variables. |
Examples
factor f1.ml group01
declares the factor object F1 then estimates the factor model using the correlation matrix for the series in GROUP01 by the method of maximum likelihood.
f1.ml group01 @partial ser1 ser2
estimates the same specification using the partial correlation for the series in GROUP01, conditional on the series SER1 and SER2.
f1.ml(n=parallel, priors=max) x y z
uses parallel analysis to determine the number of factors for a model estimates from the series X, Y, and Z, and uses the maximum absolute correlations to determine the initial uniqueness estimates.
f1.ml(n=scree) sym01 424
estimates the factor model using the observed matrix SYM01. The number of observations is 424, and the number of factors is determined using the standard error scree.
Cross-references
See
“Factor Analysis” for a general discussion of factor analysis. The various estimation methods are described in
“Estimation Methods”.
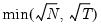 ), “size” (
), “size” (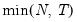 ), “user” (user specified value), where
), “user” (user specified value), where 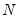 is the number of series and
is the number of series and 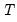 is the number of observations.
is the number of observations.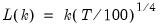
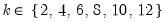 and let
and let 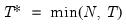 ; then the default maximum lag is given by
; then the default maximum lag is given by