transform=arg (default=“dwt”) | Wavelet transform type: “dwt” (discrete wavelet transform – DWT), “modwt” (maximum overlap DWT – MODWT), “mra” (DWT multiresolution analysis – DWT MRA), or “momra” (MODWT MRA). Note that when performing DWT or MRA, if the series length is not dyadic, a dyadic fix may be set with the “fixlen=” option |
fixlen=arg (default=“mean”) | Fix dyadic lengths in DWT and MRA transforms: “zeros” (pad remainder with zeros), “mean” (pad remainder with mean of series), “median” (pad remainder with median of series), “shorten” (cut series length to dyadic length preceding series length). |
maxscale=integer (default = max possible) | Maximum scale for wavelet transform. The max possible is obtained as follows. Let  denote the series length and decompose denote the series length and decompose  into its dyadic component and a remainder: into its dyadic component and a remainder: 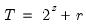 , ,  . The default maxscale . The default maxscale 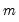 is then set with the following rules: is then set with the following rules:DWT: (1) if 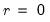 then then 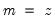 , otherwise (2) if expanding the series, , otherwise (2) if expanding the series, 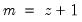 and (3) if contracting the series and (3) if contracting the series 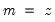 . .MODWT: 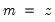 . . |
filter=arg (default=“h”) | Wavelet filter class: “h” (Haar), “d” (Daubechies), “la” (least asymmetric). If “filter=h” or “filter=la”, the filter length may be specified using “flen=”. Wavelet filter boundary conditions are specified using the “bound=” option |
flen=integer | Wavelet filter excess length as an even number between 2 and 20. For use when “filter=d” (default= 4) or “filter=la” (default=8). |
bound=arg (default = “p”) | Filter boundary handling: “p” (periodic), “r” (reflective). |
hidebound | Wavelet filter coefficients affected by the boundary will not be highlighted in the output graphs. |
prompt | Force the dialog to appear from within a program. |
p | Print results. |