Threshold Estimation in EViews
To estimate a threshold regression in EViews, select or from the main EViews menu, then select in the drop-down menu. Alternatively, type threshold in the command window and press . You will see the following dialog:
There are two tabs in the threshold regression dialog: and . We discuss each of the pages in turn.
Specification
There are three distinct sections in the threshold regression page: , , and specification. Since the sample specification should be familiar, we will focus on the first two sections.
In the first edit field of the section you should enter the dependent variable followed by a list of variables with threshold specific coefficients. The list of explanatory variables may include lagged series and ranges of lagged series specified with the word “to” (lag ranges are common in threshold regression models). In the second edit field, you may optionally specify a list of non-threshold varying regressors.
Next, in the edit field, you should a specification for one or more threshold variables. You may enter this specification as a single integer or integer pairs, or you may provide a list of variables:
• If you enter a single integer, EViews will interpret the value as the delay parameter in a SETAR model. Thus, if your dependent variable is Y and you enter a “3” in the edit field, EViews will use Y(-3) as the threshold variable.
• If you enter a single variable name, EViews will use that variable as the threshold variable. Thus, if you enter “W”, EViews will estimate the specification using the series W as the threshold variable.
• If you enter one or more lag pairs, EViews will use model selection to determine the best delay parameter amongst all of the implied lag values. Thus, if you enter “1 4 7 9”, EViews will estimate SETAR models with delay parameters between 1 and 4 and between 7 and 9, (threshold variables {Y(-1), Y(-2), Y(-3), Y(-4), Y(-7), Y(-8), Y(‑9)}), and determine the specification that minimizes the sum-of-squared residuals.
• If you specify more than one variable, by providing a list of names, entering a group name, or using wildcard expressions, EViews will estimate TR models using each variable as the threshold variable and will employ model selection to choose the specification that minimizes the sum-of-squares.
The model selection criterion is the sum of the squares of the residuals (SSR). Also note that your threshold specification may not mix integer specifications and explicit variable lists.
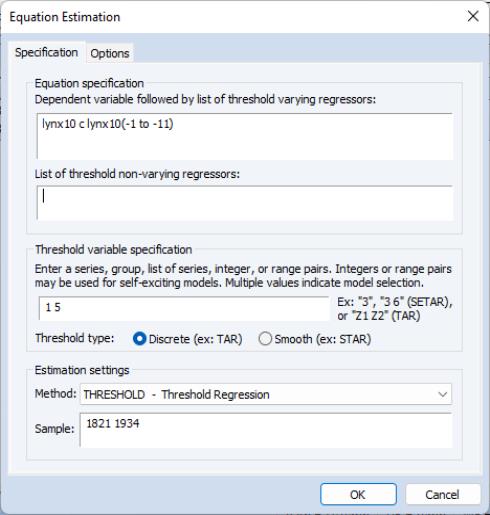
In the example depicted above, we specify a threshold regime specific AR(11) specification for LYNX_TRANSF and enter the range pair “1 5” in the edit field. The result is a SETAR model where we will perform model selection for the threshold variable using lags of LYNX_TRANSF from
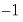
to
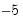
.
Options
The page contains additional settings for the calculation of the coefficient covariance matrix, the determination of thresholds, and the coefficient name. Most of the settings are identical to those found in breakpoint least squares, and extensive discussion may be found elsewhere (
“Estimating Least Squares with Breakpoints in EViews”).
We offer a brief description of the threshold specification methods below.
Threshold Value Estimation Methods
EViews offers a number of options for choosing the number and location of the threshold values.
If the number of thresholds is known it can be entered as one of the “Fixed number” specification options.
Before describing the other methods, it is important to note that EViews uses the methodologies of Bai and Perron (1998), and not the fixed regressor bootstrap testing proposed by Hansen (1999), to determine the number of thresholds. We caution you that the approaches based on testing should be viewed as informal in the TAR setting as the lagged endogenous regressors in the model are themselves subject to structural breaks which violates the assumptions for the Sup-F statistics (Hansen, 2000; Hansen, 1999).
For a given
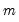
, global estimation of thresholds compares the SSRs for all possible sets of
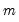
threshold values. The following global methods are used to identify threshold values and the associated regression coefficients. In the first two methods the number of thresholds is unknown and user must specify the maximum number of thresholds allowed. In the last case the desired number of thresholds must be entered.
• Global
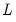
thresholds versus none
• Minimizing the information criteria
• Fixed number - global
Threshold values may also be estimated sequentially by finding an initial threshold value that minimizes the residual sums of squares, then searching for additional values (given the initial value) that minimize the SSR until the desired number of thresholds, possibly determined through testing, is obtained. Sequential tests are used in the following methods. Again, in the first two methods, the number of thresholds is not known and the user must enter the maximum number of thresholds allowed. In the last case, the user must enter the desired number of thresholds:
• Sequential
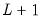
breaks vs.
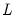
• Sequential tests all subsets
• Fixed number - sequential
The global tests are mixed with sequential testing in the
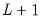
versus global
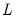
method.
Additional details for each of these methods may be found in the discussion of breakpoint regression (
“Background”) and breakpoint testing (
“Multiple Breakpoint Tests”).

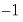 to
to  .
.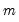 , global estimation of thresholds compares the SSRs for all possible sets of
, global estimation of thresholds compares the SSRs for all possible sets of 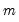 threshold values. The following global methods are used to identify threshold values and the associated regression coefficients. In the first two methods the number of thresholds is unknown and user must specify the maximum number of thresholds allowed. In the last case the desired number of thresholds must be entered.
threshold values. The following global methods are used to identify threshold values and the associated regression coefficients. In the first two methods the number of thresholds is unknown and user must specify the maximum number of thresholds allowed. In the last case the desired number of thresholds must be entered.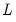 thresholds versus none
thresholds versus none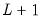 breaks vs.
breaks vs. 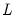
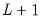 versus global
versus global 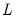 method.
method.