Johansen’s cointegration test for the series in the var object.
Syntax
var_name.coint(options) [lag_spec] [@ x1 x2 x3 ...] [@exogsr sx1 sx2 sx3 ...] [@exoglr lx1 lx2 lx3 ...] [@exogboth bx1 bx2 bx3 ...]
uses the coint keyword followed by options, and optionally,
• a lag_spec consisting of one or more pairs of lag intervals, where the lag orders are for the differences in the error correction representation of the VEC, not the levels representation of the VAR.
• an “@”-sign or “@exogsr” followed by a list of exogenous variables in the short-run equation only
• “@exoglr” followed by a list of exogenous variables in the long-run relation only
• “@exogboth” followed by a list of exogenous variables in both the long-run relation and the short-run equations
The coint command tests for cointegration among the series in the var object using the lag spec, exogenous variables, and if relevant, deterministic spec and VEC restrictions specified in estimation.
• You may provide explicit lag_spec to override the one used in estimation.
Note that if the estimation lags were for a VAR specification in levels, the default lag_spec will be the original spec adjusted for the error correction differences. Thus, if the original estimation was for a “1 4” VAR, the default lag_spec will be “1 3”.
• You may provide a “determ=” option to override an existing VEC deterministic trend specification.
• You may explicitly list any type of exogenous variable to override the entire existing specification for the exogenous variables.
The output for cointegration tests displays p-values for the rank test statistics. These p-values are computed using the response surface coefficients as estimated in MacKinnon, Haug, and Michelis (1999). The 0.05 critical values are also based on the response surface coefficients from MacKinnon-Haug-Michelis. Note: the reported critical values assume no exogenous variables other than an intercept and trend.
Options
Deterministic Trend Option
There are 8 different deterministic trend assumptions that you may specify using the “determ=arg” option.
These cases correspond to whether the intercept (“c”) and the trend (“t”) are either
• not included (“n”)
• in the long-run cointegrating relation only (“l”)
• in the short-run equation only (“s”)
• in both the long and short-run equations (“b”)
The values of arg are text shortcuts formed by joining a text shortcut for the intercept specification with a text shortcut for the trend specification.
The individual intercept and trend specifications are formed by joining the “c” and the “t” with the appropriate letter describing inclusion in the long and short-run equations.
For example,
• “cb” indicates that the constant is in both the long and short-run equation
• “tl” indicates that the trend is in the long-run cointegrating equation only
so that
• “cbtl” indicates that the constant is in both the long and short-run and the trend is in the long-run only
Using this convention (along with a special “none” option), we may easily describe options arguments for all 8 deterministic cases:
cntn, none | Case 1: No deterministic terms. Corresponding VAR model has no deterministic terms. |
cltn | Case 2: Restricted constant. Constant only in the cointegrating relations. Corresponding VAR has a constant. |
cbtn (default) | Case 3 (JHJ): Unrestricted constant Constant included both in the short-run equation and (artificially) in the cointegrating relations via orthogonalization. Corresponding VAR has a constant and trend. |
cstn | Case 3: Unrestricted constant Constant only in the short-run equation. Corresponding VAR has a trend. |
cbtl | Case 4 (JHJ): Unrestricted constant and restricted trend Constant included both in the short-run equation and (artificially) in the cointegrating relations via orthogonalization, and trend included only in the cointegrating relations. Corresponding VAR has a constant and trend. |
cstl | Case 4: Unrestricted constant and restricted trend Constant only in the short-run equation, and trend only in the cointegrating relation. Corresponding VAR has a trend. |
cbtb | Case 5 (JHJ): Unrestricted constant and trend Constant and trend both included in the short-run equation and (artificially) in the cointegrating relations via orthogonalization. Corresponding VAR has a constant, linear, and quadratic trend. |
csts | Case 5: Unrestricted constant and trend Constant and trend both included in the short-run equation. Corresponding VAR has a linear and quadratic trend. |
or you may use the “determsummary” option to compute tests under all deterministic assumptions.
Other Options
determsummary | Summarize all deterministic trend cases. |
restrict | Impose restrictions as specified by the
Var::append proc, or the “restspec=” option. |
restspec="spec" | Define the restricted VEC specification where spec is a space a space delimited list of VEC coefficient restrictions. |
m = integer, maxit = integer | Maximum number of iterations for restricted estimation (only valid if you choose the restrict option). |
c = scalar, cvg = scalar | Convergence criterion for restricted estimation. (only valid if you choose the restrict option). |
save = mat_name | Stores test statistics as a named matrix object. The save= option stores a 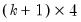 matrix, where 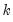 is the number of endogenous variables in the VAR. The first column contains the eigenvalues, the second column contains the maximum eigenvalue statistics, the third column contains the trace statistics, and the fourth column contains the log likelihood values. The i-th row of columns 2 and 3 are the test statistics for rank 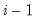 . The last row is filled with NAs, except the last column which contains the log likelihood value of the unrestricted (full rank) model. |
cvtype=ol | Display 0.05 and 0.01 critical values from Osterwald-Lenum (1992). This option reproduces the output from version 4. The default is to display critical values based on the response surface coefficients from MacKinnon-Haug-Michelis (1999). Note that the argument on the right side of the equals sign are letters, not numbers 0-1). |
cvsize=arg (default=0.05) | Specify the size of MacKinnon-Haug-Michelis (1999) critical values to be displayed. The size must be between 0.0001 and 0.9999; values outside this range will be reset to the default value of 0.05. This option is ignored if you set “cvtype=ol”. |
prompt | Force the dialog to appear from within a program. |
p | Print results. |
Examples
var1.coint(determ=cbtl) 1 12 @
carries out the Johansen test for the series in the var object named VAR1 using lags 1 to 12. The “@”-sign without a list of exogenous variables ensures that the test does not include any exogenous variables in VAR1.
Cross-references
See
“Johansen Cointegration Test” for details on the Johansen test.
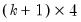 matrix, where
matrix, where 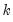 is the number of endogenous variables in the VAR. The first column contains the eigenvalues, the second column contains the maximum eigenvalue statistics, the third column contains the trace statistics, and the fourth column contains the log likelihood values. The i-th row of columns 2 and 3 are the test statistics for rank
is the number of endogenous variables in the VAR. The first column contains the eigenvalues, the second column contains the maximum eigenvalue statistics, the third column contains the trace statistics, and the fourth column contains the log likelihood values. The i-th row of columns 2 and 3 are the test statistics for rank 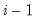 . The last row is filled with NAs, except the last column which contains the log likelihood value of the unrestricted (full rank) model.
. The last row is filled with NAs, except the last column which contains the log likelihood value of the unrestricted (full rank) model.