Estimate VAR specification.
Syntax
var_name.ls(options) lag_pairs endog_list [@ exog_list] [@restrict restrict_list]
ls estimates an unrestricted VAR using equation-by-equation OLS. You must specify the order of the VAR (using one or more pairs of lag intervals), and then provide a list of series or groups to be used as endogenous variables. You may include exogenous variables such as trends and seasonal dummies in the VAR by including an “@-sign” followed by a list of series or groups. A constant is automatically added to the list of exogenous variables; to estimate a specification without a constant, you should use the option “noconst”.
The
restrict_list is a comma-separated list of text restrictions in the form described below and in greater detail in
“VARs With Linear Constraints”.
Restriction text expressions use the following “@” keywords to refer to individual coefficient matrix elements:
@l#(r, c) | Element (r, c) of the lag # coefficient matrix. |
@e#(r) | Element r of the exogenous variable # coefficient vector. |
@e(X, r) | Element r of the exogenous variable X coefficient vector |
Note that the canonical names (“L#”, “E#”, “E(X)”) that refer to lag matrices and exogenous variable vectors are preceded by “@” to avoid ambiguity.
For example, we may have:
@L1(1,1) = 0
@L2(2,2) = @L1(3,3) / 2
@L2(1,1) + @L4(2,1) = 1
@E(C, 1) = 0
@E(X, 2) = @E(C, 2)
@E1(1) + @E1(2) = 1
In addition, you may use text expressions to refer to parts of lag coefficient matrices and to impose specialized restrictions,
| Restricts all elements of matrix W similar to a pattern matrix. Element ordering matches the vectorization of the matrix, i.e., the elements of the first column, followed by the second column, followed by the third column, etc. |
@diag(W) | Restricts W to be a diagonal matrix, i.e., off-diagonal elements are zero. The diagonal elements are unrestricted. |
@diag(W) = n | Restricts W to be a diagonal matrix with elements on the diagonal restricted to be n. |
@lower(W) | Restricts W to be a lower triangular matrix, i.e., elements above the diagonal are zero. |
@unitlower(W) | Restricts W to be a unit lower triangular matrix, i.e., elements above the diagonal are zero and elements on the diagonal are one. |
@upper(W) | Restricts W to be an upper triangular matrix, i.e., elements below the diagonal are zero. |
@unitupper(W) | Restricts W to be a unit upper triangular matrix, i.e., elements below the diagonal are zero and elements on the diagonal are one. |
@row(W, r) = n | Restricts the elements in row r of W to be n. |
@col(W, c) = n | Restricts the elements in column c of W to be n. |
where
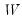
is a reference to a canonical matrix name (
e.g., “L1”, “L3”).
When a “@vec” restriction is included in the restriction list, its own list of values must be enclosed in double quotes, as in
@vec(W) = "1, 2, 3, 4"
Options
General options
noconst | Do not include a constant in exogenous regressors list for VARs. |
prompt | Force the dialog to appear from within a program. |
p | Print basic estimation results. |
Restricted VAR options
noiter | Perform GLS with a single iteration. |
m=integer | Set maximum number of iterations. If iteration and “m=0” then estimation will be by OLS. |
c=scalar | Set convergence criterion. |
showopts / ‑showopts | [Do / do not] display the estimation options in the estimation output. |
Examples
var mvar.ls 1 3 m1 gdp
declares and estimates an unrestricted VAR named MVAR with two endogenous variables (M1 and GDP), a constant and 3 lags (lags 1 through 3).
mvar.ls(noconst) 1 3 ml gdp
estimates the same VAR, but with no constant.
mvar.ls 1 2 dlog(invest) dlog(income) dlog(cons) @restrict @vec(l1) = "na, 0, na, 0, na, na, na, na, na", @vec(l2) = "na, na, na, 0, 0, na, na, na, na"
estimates a VAR with pattern restrictions on elements of the first and second lag matrices.
Cross-references
See also
Var::ec and
Var::bvar for estimation of error correction models and Bayesian VAR estimation.
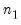 ,
,  ,
, 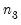 , ...
, ...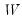 is a reference to a canonical matrix name (
is a reference to a canonical matrix name (