Working with Equations
The follow description outlines common views and procedures that are available for an estimated equation. Specialized estimators may support only a subset of these views and procs, while perhaps offering others.
Views of an Equation
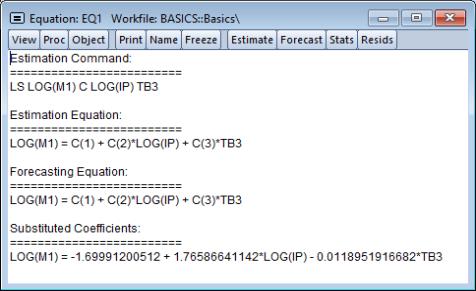
• . Displays the equation in three basic forms: EViews command form showing the command associated with the equation, as an algebraic equation with symbolic coefficients, and as an equation with a text representation of the estimated values of the coefficients.
You can cut-and-paste from the representations view into any application that supports the Windows clipboard.
• . Displays the equation output results described above.
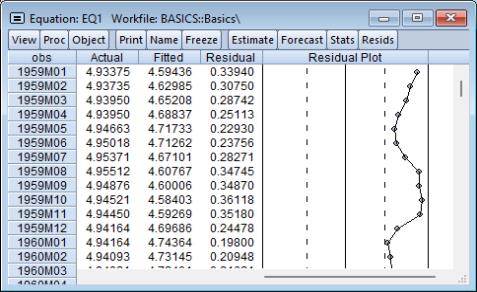
• . These views display the actual and fitted values of the dependent variable and the residuals from the regression in tabular and graphical form. displays these values in table form.
Note that the actual value is always the sum of the fitted value and the residual. displays a standard EViews graph of the actual values, fitted values, and residuals, along with dotted lines showing at plus and minus one estimated standard error. plots only the residuals, while the plots the residuals divided by the estimated residual standard deviation.
• . Provides views which describe the estimated ARMA structure of your residuals. Details on these views are provided in
“ARMA Structure”.
• . Provides views which describe the gradients of the objective function and the information about the computation of any derivatives of the regression function. Details on these views are provided in
Appendix D. “Gradients and Derivatives”.
• . Displays the covariance matrix of the coefficient estimates as a spreadsheet view. To save this covariance matrix as a matrix object, use the @coefcov member of the equation, as in
sym mycov = eq1.@coefcov
Procedures of an Equation
• . Brings up the dialog box so that you can modify your specification. You can edit the equation specification, or change the estimation method or estimation sample.
• . Saves the residuals from the regression as a series in the workfile. Depending on the estimation method, you may choose from three types of residuals: ordinary, standardized, and generalized. For ordinary least squares, only the ordinary residuals may be saved.
• Creates an untitled group comprised of all the variables used in the equation (with the exception of the constant).
• . Creates a group containing the gradients of the objective function with respect to the coefficients of the model.
• Creates a group containing the derivatives of the regression function with respect to the coefficients in the regression function.
• . Creates an untitled model containing a link to the estimated equation if a named equation or the substituted coefficients representation of an untitled equation. This model can be solved in the usual manner. See
“Models” for information on how to use models for forecasting and simulations.
• Places the estimated coefficients of the equation in the coefficient vector. You can use this procedure to initialize starting values for various estimation procedures.
Residuals from an Equation
The residuals from the default equation are stored in a series object called RESID. RESID may be used directly as if it were a regular series, except in estimation.
RESID will be overwritten whenever you estimate an equation and will contain the residuals from the latest estimated equation. To save the residuals from a particular equation for later analysis, you should save them in a different series so they are not overwritten by the next estimation command. For example, you can copy the residuals into a regular EViews series called RES1 using the command:
series res1 = resid
There is an even better approach to saving the residuals. Even if you have already overwritten the RESID series, you can always create the desired series using EViews’ built-in procedures if you still have the equation object. If your equation is named EQ1, open the equation window and select , or enter:
eq1.makeresid res1
to create the desired series.
Storing and Retrieving an Equation
As with other objects, equations may be stored to disk in data bank or database files. You can also fetch equations from these files.
Equations may also be copied-and-pasted to, or from, workfiles or databases.
EViews even allows you to access equations directly from your databases or another workfile. You can estimate an equation, store it in a database, and then use it to forecast in several workfiles.
See
“Object Basics” and
“EViews Databases” for additional information about objects, databases, and object containers.
Using Estimated Coefficients
The coefficients of an equation are listed in the representations view. By default, EViews will use the C coefficient vector when you specify an equation, but you may explicitly use other coefficient vectors in defining your equation.
These stored coefficients may be used as scalars in generating data. While there are easier ways of generating fitted values (see
“Forecasting from an Equation”), for purposes of illustration, note that we can use the coefficients to form the fitted values from an equation. The command:
series cshat = eq1.c(1) + eq1.c(2)*gdp
forms the fitted value of CS, CSHAT, from the OLS regression coefficients and the independent variables from the equation object EQ1.
Note that while EViews will accept a series generating equation which does not explicitly refer to a named equation:
series cshat = c(1) + c(2)*gdp
and will use the existing values in the C coefficient vector, we strongly recommend that you always use named equations to identify the appropriate coefficients. In general, C will contain the correct coefficient values only immediately following estimation or a coefficient update. Using a named equation, or selecting guarantees that you are using the correct coefficient values.
An alternative to referring to the coefficient vector is to reference the
@coefs elements of your equation (see
“Selected Keywords that Return Scalar Values”). For example, the examples above may be written as:
series cshat=eq1.@coefs(1)+eq1.@coefs(2)*gdp
EViews assigns an index to each coefficient in the order that it appears in the representations view. Thus, if you estimate the equation:
equation eq01.ls y=c(10)+b(5)*y(-1)+a(7)*inc
where B and A are also coefficient vectors, then:
• eq01.@coefs(1) contains C(10)
• eq01.@coefs(2) contains B(5)
• eq01.@coefs(3) contains A(7)
This method should prove useful in matching coefficients to standard errors derived from the
@stderrs elements of the equation (see
“Equation Data Members”). The
@coefs elements allow you to refer to both the coefficients and the standard errors using a common index.
If you have used an alternative named coefficient vector in specifying your equation, you can also access the coefficient vector directly. For example, if you have used a coefficient vector named BETA, you can generate the fitted values by issuing the commands:
equation eq02.ls cs = beta(1) + beta(2)*gdp
series cshat = beta(1) + beta(2)*gdp
where BETA is a coefficient vector. Again, however, we recommend that you use the @coefs elements to refer to the coefficients of EQ02. Alternatively, you can update the coefficients in BETA prior to use by selecting from the equation window. Note that EViews does not allow you to refer to the named equation coefficients eq02.beta(1) and eq02.beta(2). You must instead use the expressions, eq02.@coefs(1) and eq02.@coefs(2).